ディフィー・ヘルマン鍵共有って何だろう？

皆さん、こんにちは。技術開発グループのn-ozawanです。
日本酒のひやおろしが解禁され始めましたね。秋の訪れを感じます。

前回は公開鍵暗号方式とRSAについてお話ししました。公開鍵暗号方式は共通鍵を通信間で共有する方法の１つであるものの、公開鍵暗号方式であるRSAは鍵共有としては非推奨となっています。現在はDH（ディフィー・ヘルマン鍵共有）もしくはECDHD（楕円曲線ディフィー・ヘルマン鍵共有）が使われています。今回はそのディフィー・ヘルマン鍵共有についてお話しします。

ディフィー・ヘルマン鍵共有

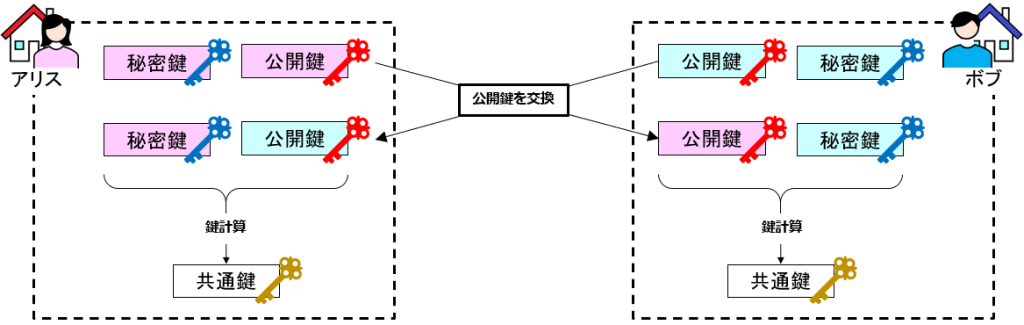
ディフィー・ヘルマン鍵共有（以降、DHと表記）は、離散対数問題という数学上の問題を利用した公開鍵暗号方式です。通信間で互いに公開鍵と秘密鍵を生成して、公開鍵を互いに交換します。そして、自身の秘密鍵と相手の公開鍵で共通鍵を生成する手法です。

離散対数問題

私自身、数学に強くないので詳細な説明は出来ませんが、簡単に離散対数問題について説明します。例えば以下の計算式があるとします。

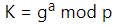
modは前回もお話しした通り、剰余演算で、割った余りを求めます。では、ここで問題です。g = 3、a = 2、p = 7の場合、Kはいくつになるのでしょうか？答えは簡単です。3 ^ 2 mod 7 なので、K = 2 になります。

では、g = 3、p = 7、K = 6、の場合、aはいくつになるのでしょうか？計算式は以下になります。

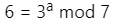
実は現状の数学では、上記のaを求めるための効率的な方法が発見されていません。もちろん、上記の式を満たすaをしらみ潰しに探せば見つけることはできます。ちなみに上記の問題ではa = 3になります。このaを求めることが難しい問題を「離散対数問題」と言います。

小さな桁数であれば今のコンピュータを駆使することでaを求めることは出来ます。しかし、大きな桁数で計算するとなると、いくら今のコンピュータとしても、aを求めるのに天文学的な時間が必要となります。これにより実質安全とみなしているわけです。

鍵共有プロセス

ディフィー・ヘルマン鍵共有の基本的な計算式は以下になります。離散対数問題は指数aを求めるのが難しいという問題でした。なので指数aは秘密鍵となります。そしてその計算結果Kが公開鍵になります。

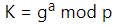
まず数値gとpを通信者間で示し合わせて決定します。アリスとボブで同じgとpを使う必要があり、数値pはとても大きな素数でなければいけません。数値gとp、そして自身の秘密鍵で計算を行い、その結果を交換します。そして、交換した計算結果Kをもとに再度計算することにより共通鍵を生成します。

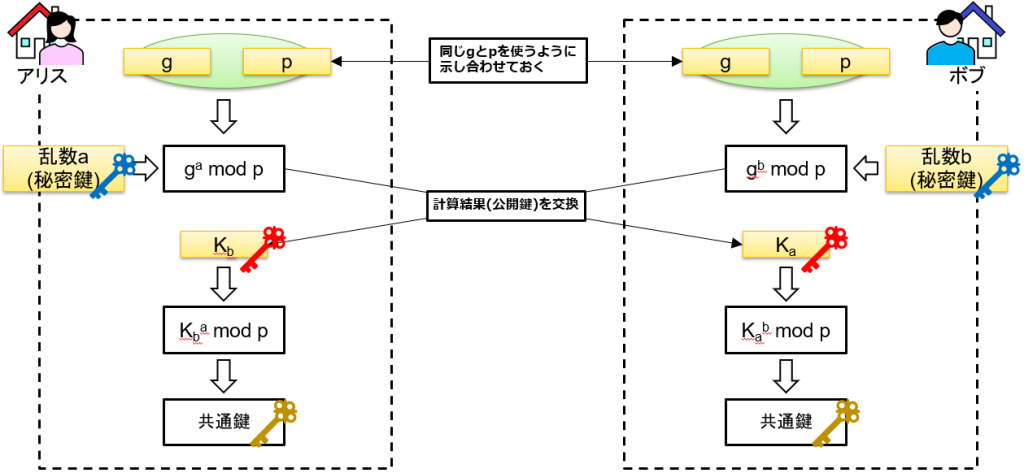
なんで相手と同じ共通鍵が生成されるの？

アリスは以下の計算式で共通鍵を求めます。

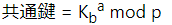
Kbはボブ側で行われた以下の式で求めます。

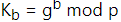
これをアリス側の計算式に当てはめます。

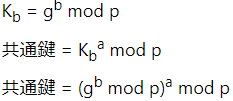
上記の式を単純化すると以下になります。

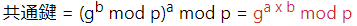
ボブ側も同様に見ていきます。

アリスもボブも、共通鍵を求める式が同じになります。離散対数問題により、盗聴者イブに推測されることなく、お互いの秘密鍵を交換して共通鍵を計算して求めているのです。

おわりに

ディフィー・ヘルマン鍵共有で安全に鍵共有が出来たとしても、前回でお話しした「なりすまし」に対する脆弱性は解消されていないことにご注意ください。「なりすまし」に対しては別途、デジタル署名などの技術が必要になります。

ではまた。