RSA 公開鍵暗号方式って何だろう?
皆さん、こんにちは。技術開発グループのn-ozawanです。
当社がブログをはじめて半年がたちました。ネタがいつまで続くのか、間違ったことを言っていないか、ドキドキしています。
先日、共通鍵暗号方式についてお話ししましたので、今回は公開鍵暗号方式についてお話ししたいと思います。
目次
公開鍵暗号方式
共通鍵暗号方式の問題点
公開鍵暗号方式をお話しする前に、共通鍵暗号方式の問題点を整理します。共通鍵暗号方式は暗号化と復号化で同じ共通鍵を利用する暗号方式です。つまり、送信元と送信先で共通鍵を共有する必要があります。共通鍵暗号方式の問題点とは、共通鍵の共有方法をどうするのか?になります。
例えば送信元のアリスから送信先のボブへ、「この共通鍵で暗号化するから、復号化してね」と言って、平文のまま共通鍵をボブへ送信すると、盗聴者のイブにあっさりと共通鍵が盗まれてしまいます。そうなってしまうと大変です。以降の暗号文はすべてイブに筒抜けになってしまいます。
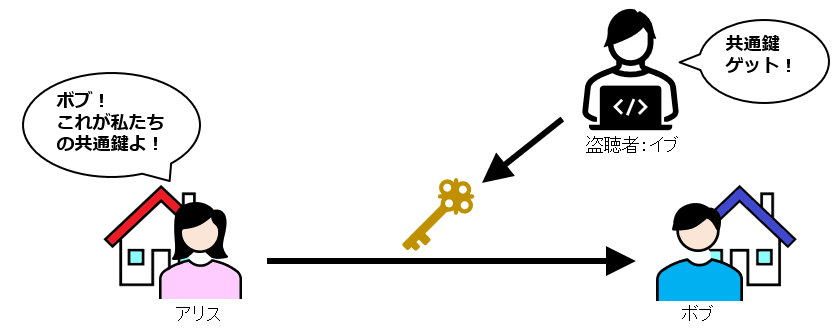
もちろんUSBメモリなどの記憶媒体に共通鍵を保存して手渡す方法もあります。しかし、これではコストがかかってしまい、実用的ではありません。そんな鍵共有の答えの1つとして公開鍵暗号方式があります。
概要
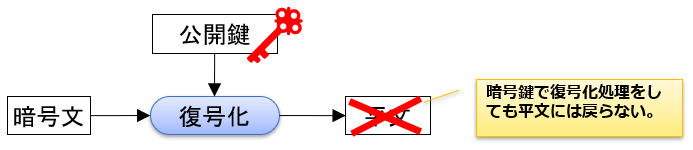
公開鍵暗号方式は公開鍵で平文を暗号化し、秘密鍵で暗号文を平文へ復号化します。公開鍵はその名の通り、外部へ公開する鍵です。秘密鍵もその名の通り、外部へ公開しない秘密の鍵です。公開鍵は平文を暗号化しますが、暗号文を復号化することは出来ませんので、仮に盗聴者イブに公開鍵を盗まれたとしても、平文を読まれることはありません。

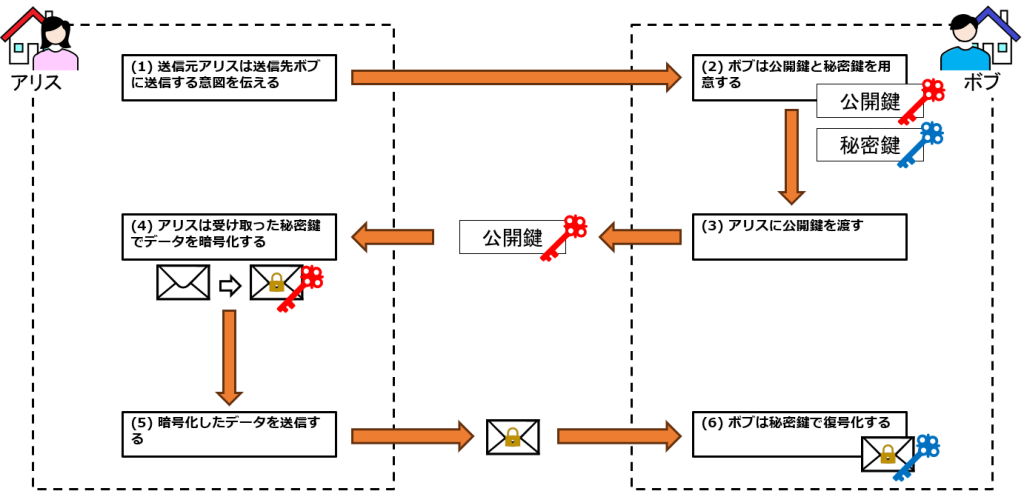
プロセス
詳細な説明は省きますが、以下の図のようなプロセスで利用します。すべての公開鍵暗号方式がこのプロセスを行っているわけではありませんが、ここでは理解の一助として掲載します。※図中の「データ」を共通鍵とすることで、通信者間で共通鍵を共有します。
RSA
公開鍵暗号方式の1つ「RSA」についてお話しします。RSAは3人の発明者(Ron Rivest、Adi Shamir、Leonard Adleman)の頭文字をとって命名された公開鍵暗号方式です。現在、RSAは鍵共有としては非推奨となっている暗号方式です。ですが、デジタル署名では未だ利用されています。
暗号化と復号化
RSAの暗号化処理は以下の式により行われます。modは剰余演算で、割った余りを求めます。以下の式にて、EとNが公開鍵に該当します。
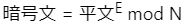
RSAの復号化処理は以下の式により行われます。以下の式でDが秘密鍵に該当します。
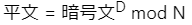
実際に暗号化と復号化をしてみた図が以下になります。秘密鍵で復号化出来ていることと、公開鍵で復号化が出来ないことが確認できるかと思います。
RSAによる鍵共有
先ほども述べた通り、RSAによる鍵共有は非推奨となっています。RSAによる鍵共有は、公開鍵で共通鍵を暗号化して、秘密鍵で復号化することにより鍵を共有します。しかし、アプリケーションの致命的な脆弱性などにより秘密鍵が流出した場合、仮にその脆弱性を解消し鍵を再生成したとしても、過去データはすべて解読されてしまいます。
TLS1.3ではRSAによる鍵共有は出来ないようになっています。また、電子政府推奨暗号リストでもRSAは推奨されていません。現在では、DH(ディフィー・ヘルマン鍵共有)もしくはECDHD(楕円曲線ディフィー・ヘルマン鍵共有)が鍵共有で使われています。
なりすまし攻撃
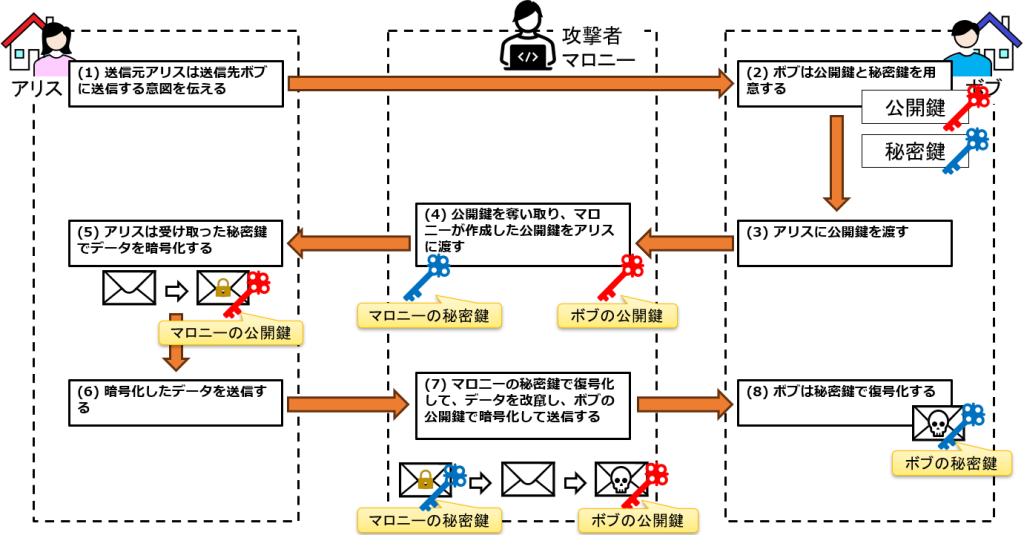
RSAに限った話ではありませんが、公開鍵暗号方式ではなりすまし攻撃に弱いという弱点があります。送信元のアリスと送信先のボブの間に、攻撃者マロニーが入り込み、公開鍵を偽造することで盗聴および改ざんを行うことが出来ます。
これを防止するには、アリスが「受け取った公開鍵が間違いなくボブであること」を検証する必要があります。これにはデジタル署名や証明書などの技術が別途必要となります。RSAはこのデジタル署名で利用されています。
おわりに
共通鍵暗号方式に続き、公開鍵暗号方式について纏めてみました。共通鍵暗号方式でもそうなのですが、数学的な知識がないと、もはや魔法にしか見えませんね。こういった専門的な知識無く、誰でも暗号化を使えるようにしてくれた数多の技術者には頭が上がりません。
ではまた。

 アイオス コーポレートブログ
アイオス コーポレートブログ










