AIを深く知りたい人のための数学 第10回 ネイピア数

皆さん、こんにちは。LP開発グループのn-ozawanです。
昨日(1/13)の東京は3月下旬並みの暖かい日になっており、スーパーでは新玉ねぎが売られてました。まだ1月中旬ながらも、春の訪れを感じます。

本題です。
機械学習で使われるシグモイド関数やソフトマックス関数では、その式中にeという定数が登場します。eはネイピア数であり、知らない人が見たらどこから来た数字なのかが分からず混乱するでしょう。今回はそんなネイピア数についてです。

※「AIを深く知りたい人のための数学」は、数学を忘れてしまったエンジニアを対象に、中学数学から思い出すことを目的としたシリーズです。

ネイピア数

概要

ネイピア数eは、約2.718281828…という値をもつ、小数点以下が無限に続く無理数です。「自然対数の底」と呼ばれており、指数関数exや自然対数ln(x)のように、数学では「自然に出てくる数」としてよく扱われます。以下はネイピア数eの定義です。

ここでのポイントは、「(1 + 1/n)をn回掛ける」という離散的な増え方を、「nを無限に大きくして回数を無限に細かくする」ことで連続的な増え方に近づけている点です。少々難しいですが、これはよく複利を例に語られています。

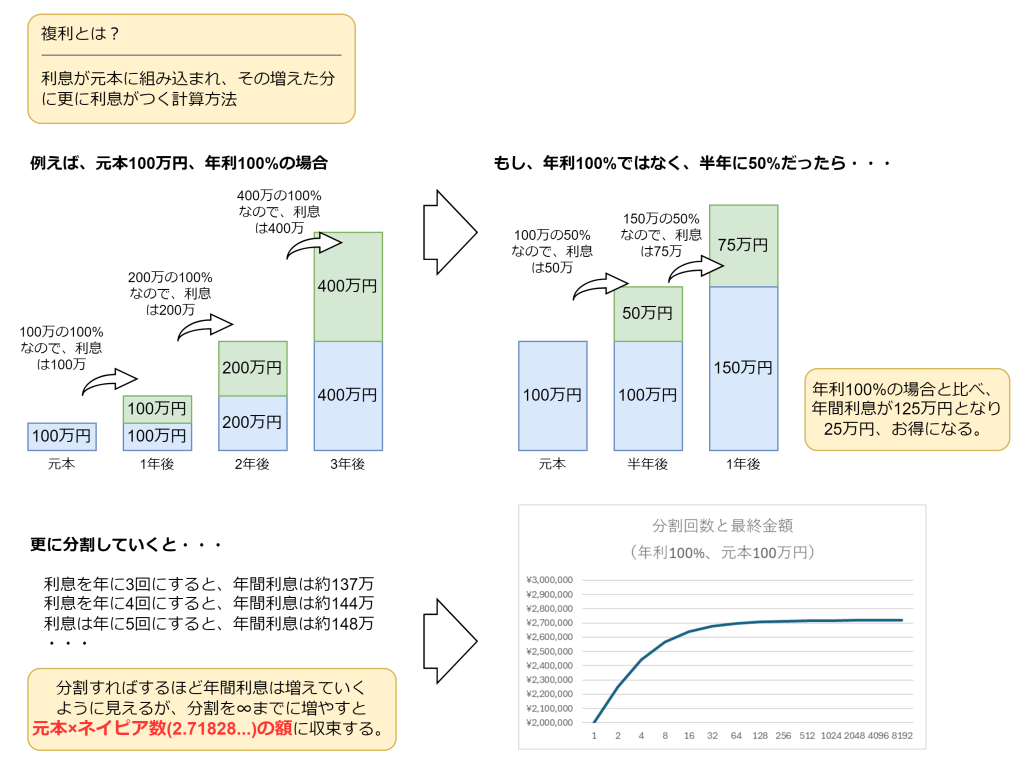
ネイピア数eは、細菌や人口の増加などの自然界の動きにも密接に結びついており、この事情から、ln(x)を「自然対数」と呼び、その底であるeを「自然対数の底」と呼びます。

AIとネイピア数

冒頭で述べた通り、機械学習、特にロジスティック回帰の分類分析ではネイピア数が使われます。また、シグモイド関数とソフトマックス関数はニューラルネットワークにおいて出力層の活性関数でも使われており、昨今のAI技術では重要な役割を持ちます。

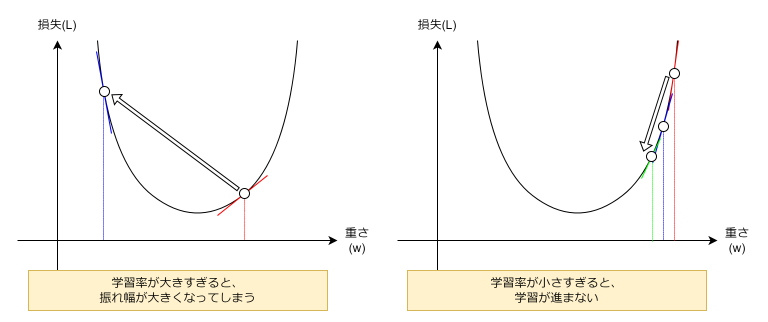
また、勾配降下法による学習において、学習率を決定するのにもネイピア数が使われるケースがあります。学習率は勾配に沿って一度にどれだけ降りていくのかを決定するハイパーパラメータです。学習初期は大きな学習率で急速に最適化し、後半は小さくして微調整した方が学習の効率が良いです。その為、時間の経過とともに学習率を減らす仕組みが必要になります。この学習率減衰の方法には、「ステップ減衰」や「コサインアニーリング」などがありますが、ネイピア数を使った指数関数的減衰と言うのがあります。

なぜネイピア数が使われるのか？

ネイピア数が特別に扱われる最大の理由は、exが微分しても形が変わらない点です。これは解析や最適化の計算を大きく簡単にします。

例えば、一般の底aに対してaxを微分すると、必ずln(a)が係数として付いて回ります（微分の公式：(ax)' = ax ln(a)）。一方で、底をeにするとその係数が1になり、式が最も簡潔になります。機械学習では勾配を計算して更新するため、この「微分がきれいに閉じる」性質が実務上の利点として効いてきます。

結果として、数式ではeが「選ばれている」というより、「単に都合がよい（計算しやすい）」「最も摩擦が少ないので自然に残っている」と言うことになります。

おわりに

ネイピア数eは、複利回数を無限に増やした極限として定義でき、「連続成長」「減衰」「確率分布」などの現象を扱う場面で必ず登場します。また、exは微分しても自分自身になり、指数と対数が確率計算や最適化と直結するため、AIの基本式で頻出します。また、ネイピア数はAI分野だけでなく、信頼度成長曲線などでも活用されています。

ではまた。