AIを深く知りたい人のための数学 第9回 極限
皆さん、こんにちは。LP開発グループのn-ozawanです。
今年の干支は丙午です。丙午は十干の「丙」と十二支の「午」が重なる60年に一度の年で、特に「火」の性質が重なるため、とてもエネルギッシュであり、大きな変革が期待される年ともいわれています。
本題です。
機械学習(主にニューラルネットワーク)で行われる勾配降下法では、その学習の収束に微分が使われます。この微分の根底には極限という考え方が必要になります(参考)。極限は「限りなくaに近づいたときにどうなるのか」を考えるため、これまでの代数的な解法とは少し異なる発想が求められます。今回はそんな極限を思い出したいと思います。
※「AIを深く知りたい人のための数学」は、数学を忘れてしまったエンジニアを対象に、中学数学から思い出すことを目的としたシリーズです。
目次
極限
極限の基本
極限は「値や入力がある点に近づくとき、出力がどこに落ち着くか」を表現する道具です。例えば1/nがあるとします。このnを限りなく大きな数字となったらどうなると思いますか?n=1であれば、1/1=1になります。n=100であれば、1/100=0.01と小さくなります。n=1,000,000であれば、1/1,000,000 = 0.000001と更に小さくなります。では、n=∞の場合はどうなるのでしょう?無限は果てしなく大きな数字です。1/∞は0になることでしょう。

関数の極限も同様です。たとえば f(x) = (x2 - 1) / (x - 1) は、x=1では計算できません。何故なら、f(1) = (12 -1) / (1 - 1) = 0/0となり、0で割ることはできないからです。では、xが限りなく1に近づくとどうなるのでしょうか。答えは2になります。

この「限りなく近づくが、必ずしも到達しない」という動きを、極限は厳密に表します。数列のようにステップが進むときの挙動にも、関数の入力がある点へ近づくときの挙動にも使います。この考え方が、微分や連続性、そして学習アルゴリズムの収束の土台を作ります。
ε-δ論法
ε-δ(イプシロン・デルタ)論法とは、「関数 f(x) が x を a に近づけたとき、値が極限値 L に近づく」という状況において、「どれくらい近づけば、どれくらい結果が近くなるか」を数値で保証します。順を追って説明します。
ε (イプシロン)とは、ゴールの近さを表す「許容誤差」です。例えば極限値Lが2となる場合、その2にどれだけ近づけば許容するのかを定めます。δ(デルタ)とは、入力の近さを表す「どれくらい a に近づけばいいか」です。結果をε以内に収めたい場合、どれぐらい x を a に近づけばいいのかの指標になります。
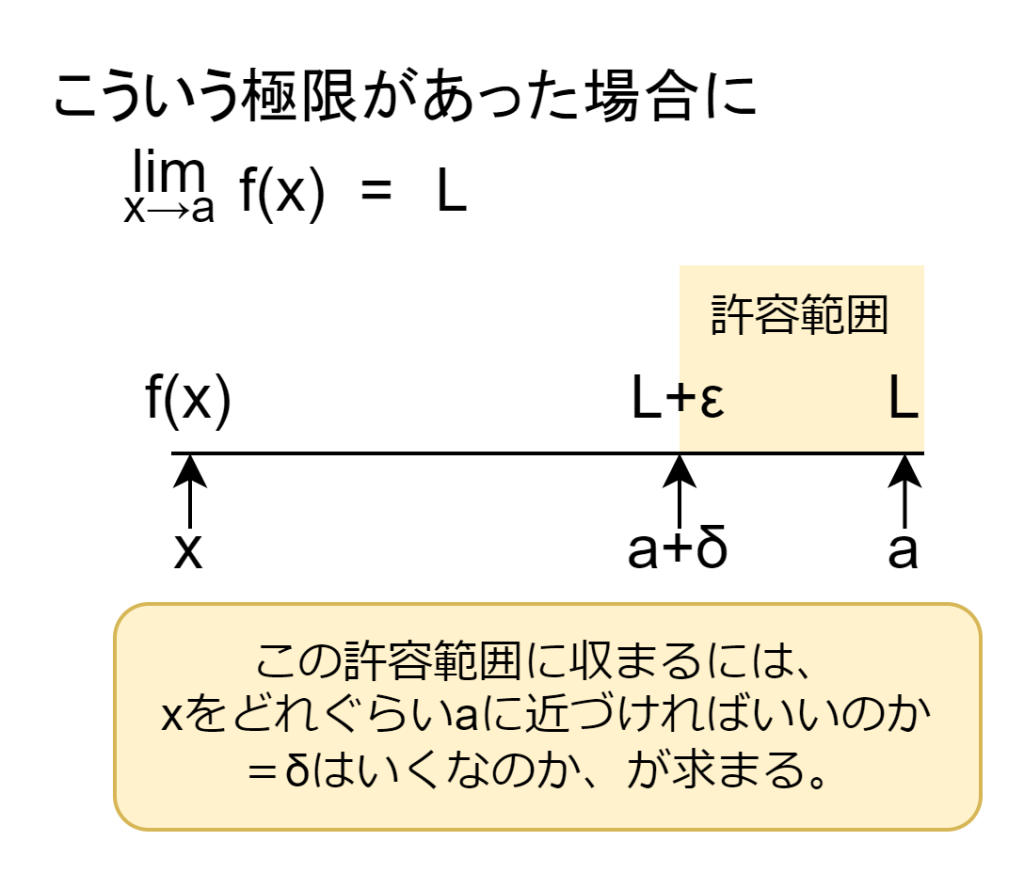
具体的な計算は省きます。AI分野でこのε-δ論法が使われることはあまり無いそうですが、「求めたい結果に近づくには、どれぐらいの調整が必要なのか」などの考え方が活きているようです。
AI分野への応用例
機械学習では「損失を小さくする」最適化の作業にて、微分が使われています。その微分は極限によって支えられているため、間接的に極限が関わっていると言えます。
また、統計の分野では大数の法則という有名な法則があります。大数の法則とは、サンプル数が増えると平均値が真の期待値に近づくという統計の基本原理です。例えば、コインを1回投げると結果は偏りますが、1万回投げると「表の割合」はほぼ50%に近づきます。これは「試行回数を無限大に近づけるほど、統計の精度が上がる」と言うことであり、極限の考え方がそのまま反映された法則です。
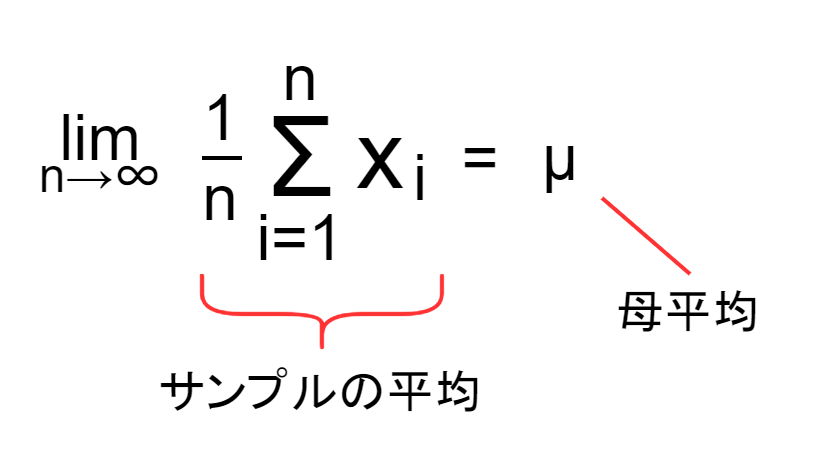
おわりに
業務アプリを開発しているときに極限を意識することはありません。しかし昨今のAI分野をはじめ、多くの技術領域で極限の考え方が使われています。
ではまた。

 アイオス コーポレートブログ
アイオス コーポレートブログ



















