AIを深く知りたい人のための数学 第7回 微分

皆さん、こんにちは。LP開発グループのn-ozawanです。
台所の水栓が壊れて水が使えなくなりました。昨年も話題にしたのですが、東京都が公開している「東京備蓄ナビ」で、災害に備えて備蓄したいと思います。

本題です。
機械学習を勉強すると必ず出てくるのが微分です。業務アプリの開発では微分を扱うことはまずありません。社会人になって微分を忘れたエンジニアは、機械学習で微分が出てきて頭に？が浮かぶのではないでしょうか。今日はそんな微分のお話です。

※「AIを深く知りたい人のための数学」は、数学を忘れてしまったエンジニアを対象に、中学数学から思い出すことを目的としたシリーズです。

微分

微分ってそもそも何？

微分は「変化量の大きさ」を数で表す道具です。入力を少しだけ動かしたとき、出力がどれくらい変わるかを測ります。

微分をイメージするには、まず「変化量の大きさ」を身近な場面で考えてみましょう。たとえば、エレベーターに乗っているとき、最初はゆっくり動き出し、途中で速くなり、止まる前にまたゆっくりになります。エレベーターが動いているこの瞬間、「今どれくらい速く進んでいるか」＝「変化量の大きさ」を知る方法が微分です。

微分は、「ほんの少し動かしたときに、どれくらい変わるのか」を調べます。たとえば、温度が時間とともにどう変わるか、株価が一瞬でどれくらい動くかなど、微分は身の回りの「変化」を読み取るための道具であり、「今この瞬間の変化」を知るための方法です。

微分の基本概念

では、どうやってその「変化」を読み取るのでしょうか。y=x2のグラフを例に、微分を説明します。

まず、y=x2のグラフは放物線です。地点A（たとえばx=1）と地点B（x=3）を考えます。AとBを直線で結ぶと、その直線の傾きは「平均的な変化量」を表します。計算すると、A(x=1, y=1)、B(x=3, y=9)なので、傾きは(9-1)/(3-1)=4です。これは「xが1から3まで増えたとき、yがどれくらい増えたか」を示します。

これを公式で表現すると以下のようになります。hはxの増加量です。f()は関数で、yを求める式になります。曲線がy=x2の場合、f(x+h)であれば、y=(x+h)2で求めます。

以上までは、2つの地点を結ぶ直線の変化量（傾き）を求める方法でした。では、任意の地点Xでの1点のみの傾きはどうなるのでしょうか？グラフに表すと、y=x2の曲線に接する直線の傾きを求めます。この傾きを知ることが微分となります。

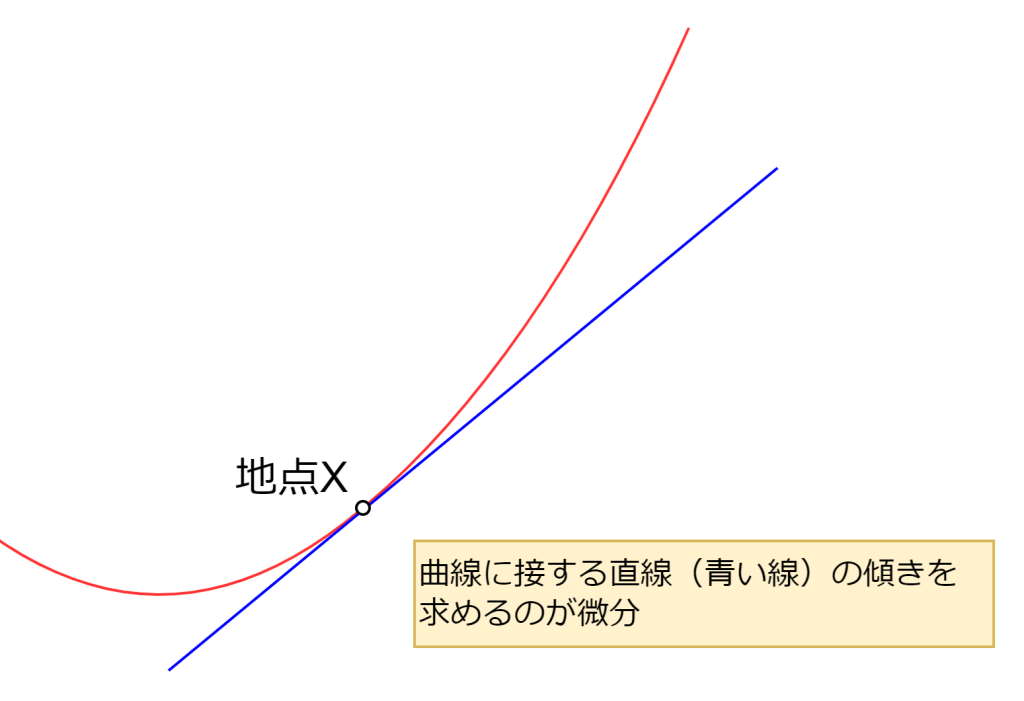
考え方としては、地点Aと地点Bが徐々に近づいて地点Xで合流するのをイメージします。その際、地点Aから地点Bへのxの変化量は限りなく0に近づきます。数式では、lim(h→0)と表記することで、hを限りなく0に近づけるという意味とします。これを以下のように計算することで、微分の導関数が求まります。

f'(x)は導関数と呼ばれているもので、その地点Xの傾きを求める式となります。y=x2の導関数はf'(x)=2xとなりますので、x=1の時の傾きは2になりますし、x=3の時の傾きは6になります。

このように、地点Aと地点Bを結ぶ傾きは平均的な変化、地点Xの傾き（微分）はその点での瞬間的な変化を表します。グラフ上では、地点Xでの接線の傾きが微分値です。微分は「今この瞬間の変化」を具体的な数値で教えてくれる道具です。

なぜ機械学習に微分が必要なのか？

微分を使うと「どちらに進めば良くなるか」が分かります。たとえば、坂道を歩いているとき、足元の傾きを感じて「上り坂か下り坂か」を判断します。微分はこの「傾き」を数値で教えてくれる道具です。坂のてっぺんや谷底では傾きがゼロになり、そこが「一番高い場所」や「一番低い場所」の目印になります。機械学習では、損失を減らすために「どちらに進めば良いか」を微分が教えてくれるので、より良い答えに近づくことができます。

機械学習は「損失を小さくする」最適化の作業です。損失関数の勾配（微分）は「どちら向きに、どのくらい動かすか」を示します。そして、傾きが0になる谷底は学習が収束する地点になるため、機械学習は傾きが0になる谷底を目指して学習を行います。この学習のためには微分は非常に都合のよい方法であり、微分がなければ、改善の方向が分からず、学習は前に進まなくなります。

おわりに

何となく微分を思い出せましたか？微分は機械学習をより理解するには必須の知識となりますので、この際に学び直すのも良いかとも思います。

ではまた。