AIを深く知りたい人のための数学 第5回 三角比

皆さん、こんにちは。LP開発グループのn-ozawanです。
今週の金曜日（11月7日）は立冬の日とされています。立冬は二十四節気で冬の始まりとされています。

本題です。
三角比とは、三角形の各辺の比のことです。三角比もIT技術を支える重要な要素ではありますが、関数などのライブラリ化により、私たちが業務アプリを開発する際に直接計算することはあまりありません。今回はそんな三角比についてのおさらいです。

三角比

三平方の定理

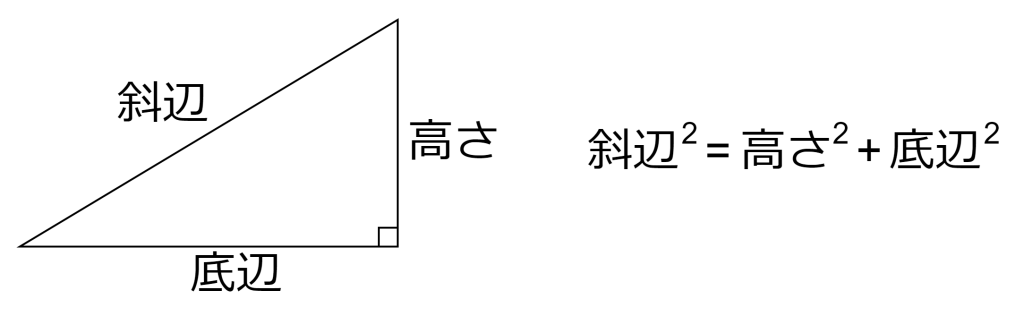
三平方の定理とは、直角三角形の3辺の長さに関する関係を表す定理です。具体的には、直角三角形の3辺は、斜辺2=高さ2+底辺2の関係になります。

この定理を使うと、45°の直角三角形と、60°の直角三角形のそれぞれの辺の長さは以下の関係になります。

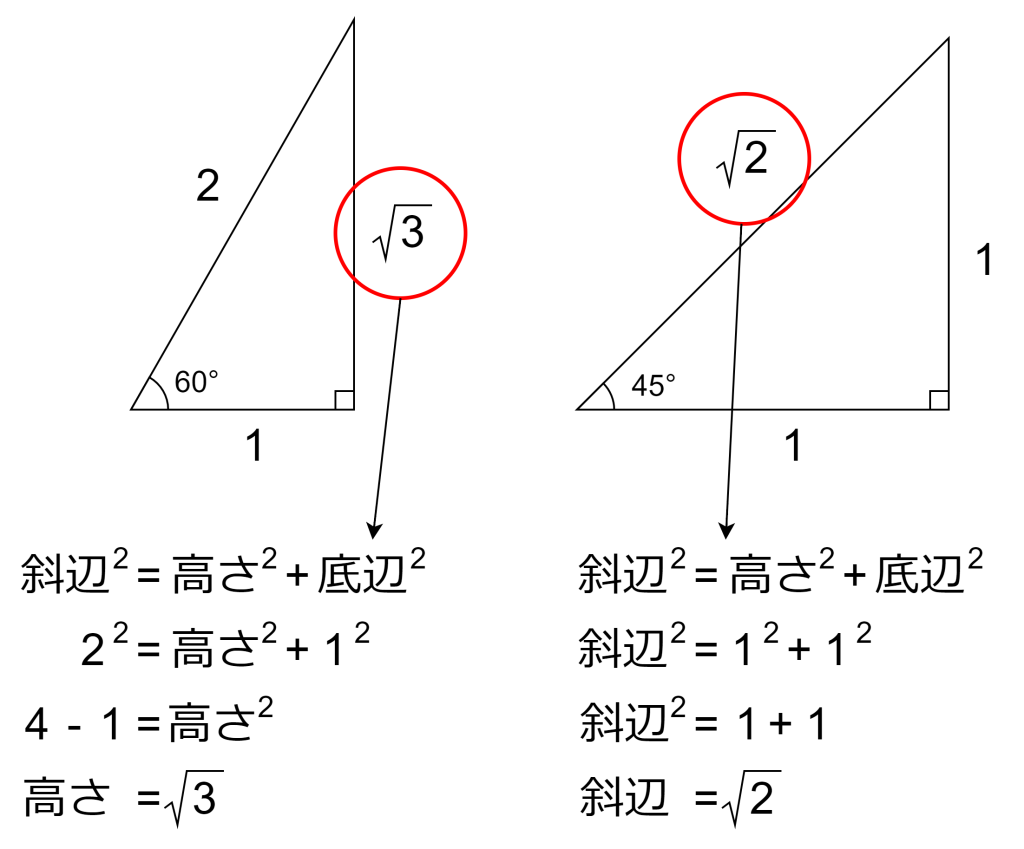
ここで注目すべきは、角度が同じ直角三角形では、辺の長さが異なっていてもその比率は常に同じであることです。つまり、角度と辺の一部が分かれば、その他の辺も分かるということになります。例えば、60°の直角三角形の場合、斜辺の長さが80cmであれば、底辺はその半分の40cmになります。つまり底辺は斜辺の1/2です。この比例関係に着目したのが三角比です。

sinΘ

sinΘは斜辺と高さの比率を表します。Θは「シータ」と読み、角度を表現します。60°の直角三角形であれば、sin 60° = 2 / √3 になります。sinΘが分かれば、高さと斜辺を求めることができます。例えば、飛行機が一定角度で上昇するとき、上昇角度が10°で1000m進んだ場合、高度は1000×sin10°であり、おおよそ174mぐらいを飛行していることが分かります。

cosΘ

cosΘは斜辺と底辺の比率を表します。60°の直角三角形であれば、cos 60° = 1 / 2 になります。cosΘが分かれば、底辺と斜辺を求めることができます。先ほどの飛行機の例で言えば、上昇角度が10°で1000m進んだ場合、実際に移動した距離は1000×cos10°であり、おおよそ985m移動したことが分かります。

tanΘ

tanΘは高さと底辺の比率を表します。60°の直角三角形であれば、tan 60° = √3 になります。tanΘが分かれば、底辺と高さを求めることができます。例えば、勾配を示す道路標識があります。勾配が10%の場合はtanΘ=0.1であることを示しており、そこから坂の角度が分かるようになります。

おわりに

測量の世界では三角比は必須レベルで使われるようです。また、三角比はCG・ゲーム分野、ロボティクス等の制御工学などでよく使われ、AI分野でも音声認識などで使われるフーリエ変換ではサイン波とコサイン波を重ね合わせで表現しています。

ではまた。