AIを深く知りたい人のための数学 第4回 多項式関数とグラフ

皆さん、こんにちは。LP開発グループのn-ozawanです。
人間は舌にある味蕾によって味を感じることができます。ナマズは全身に味蕾があり、全身から味覚を感じ取ることができます。

本題です。
AIを学び始めると1次関数や2次関数といったグラフを頻繁に目にします。私たちはプログラムで関数をコーディングしますが、グラフを描画する機会はまったくありません。今回は多項式関数と、それぞれがどうグラフで描画されるのかを思い出します。

※「AIを深く知りたい人のための数学」は、数学を忘れてしまったエンジニアを対象に、中学数学から思い出すことを目的としたシリーズです。

多項式関数

多項式関数とは、変数の累乗と定数の積の和で表される関数です。例えば、f(x) = 3x2+4x+2のような形式です。一般的には以下のような形になります。

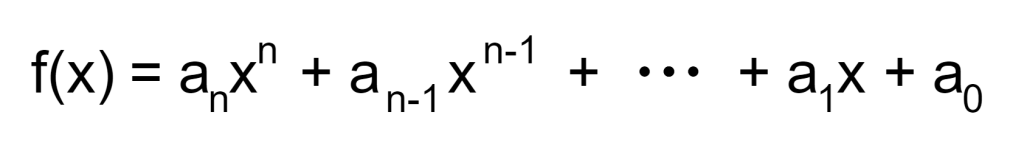
総和（Σ）で表現すると以下のようになります。

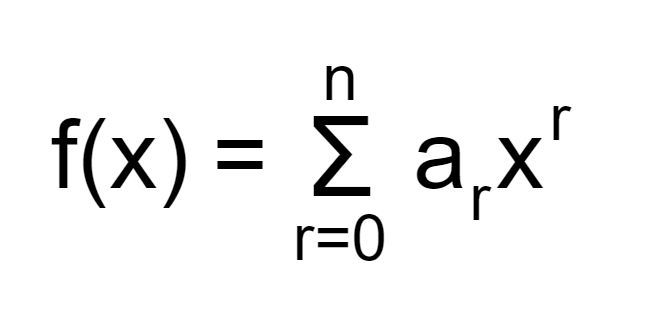
多項式関数は「多項式」と「関数」という2つの数学的な概念が組み合わさったものです。多項式とは、2つ以上の項で表現された式のことです。項とは、+や-で区切られた値です。

関数は、ある入力（変数）に対して、決まった規則に基づいて必ず1つの出力が決まる仕組みのことです。私たちプログラマには馴染みある概念ですね。多項式関数の左辺にあるf(x)が関数であることを表しています。fはfunctionであり、(x)は入力です。

1次関数

1次関数は、多項式関数において最も基本的な形の関数であり、次数が1の多項式から構成されます。1次関数は以下の式になります。

1次関数をグラフで表現すると直線になります。その際、a:傾きは直線の傾きを、b:切片は直線とy軸が交差する位置に影響を与えます。

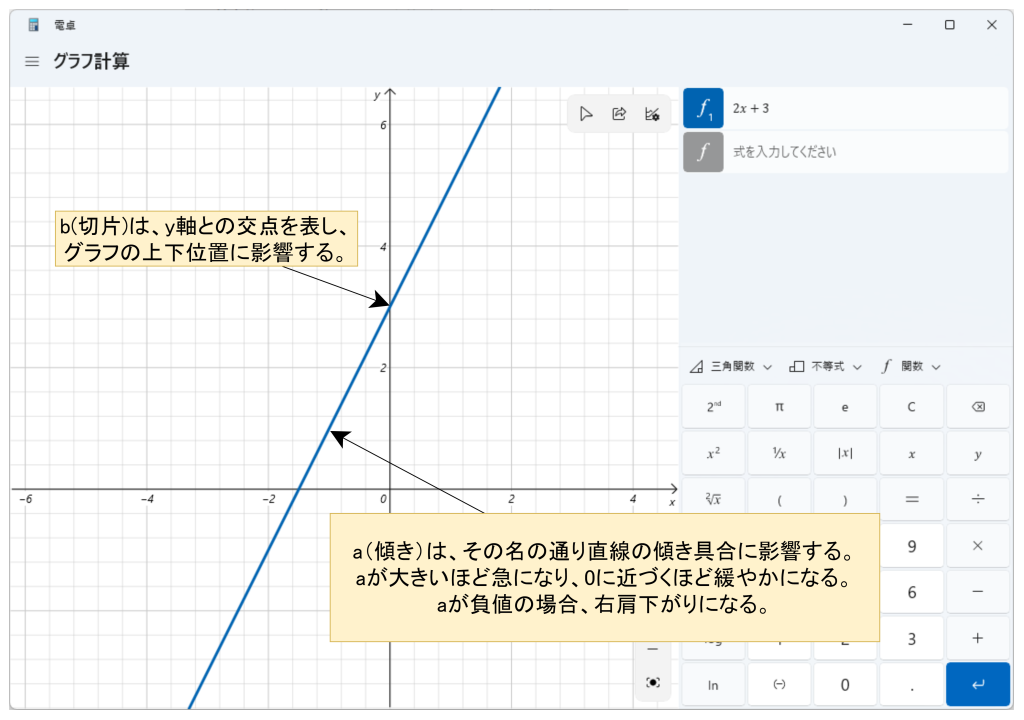
2次関数

2次関数は次数が2の多項式から構成される関数です。2次関数の基本的な式は以下になります。

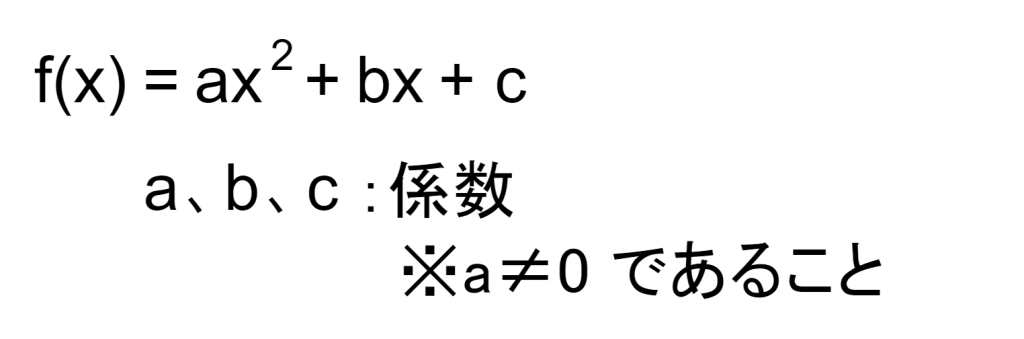
2次関数をグラフで表現すると放物線（U字型もしくは逆U字型）になります。

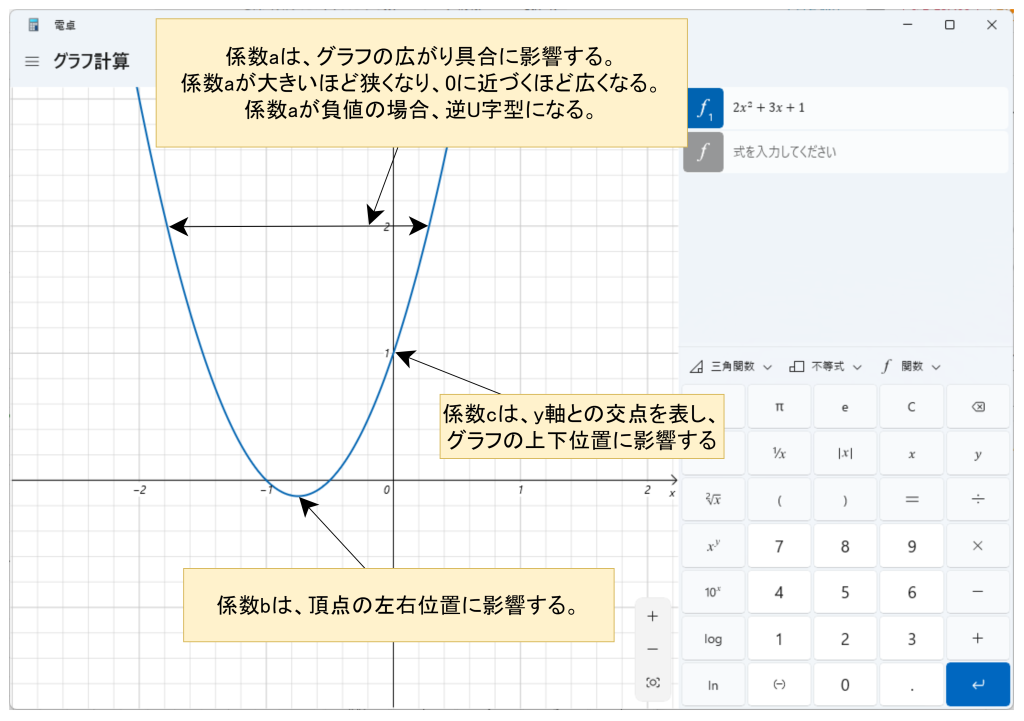
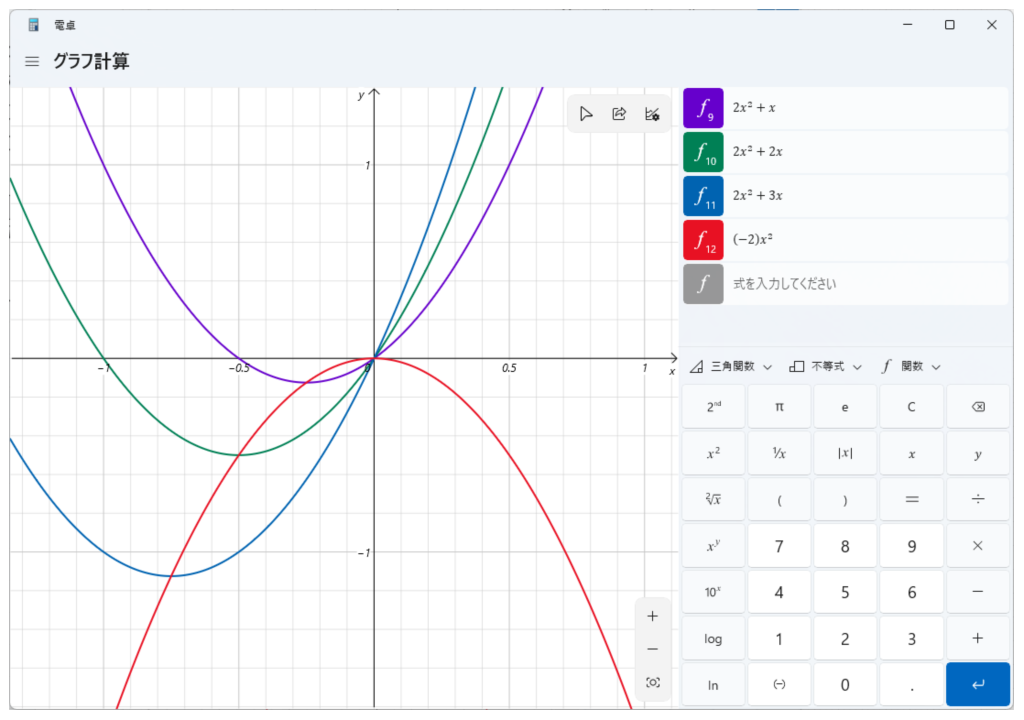
なお、2次関数における頂点のx座標は以下の式で求められます。その際、f(x)=ax2+bxにおける頂点位置は、f(x)=-ax2と同じ軌跡を辿ります。

3次関数

3次関数は次数が3の多項式から構成される関数です。3次関数の基本的な式は以下になります。

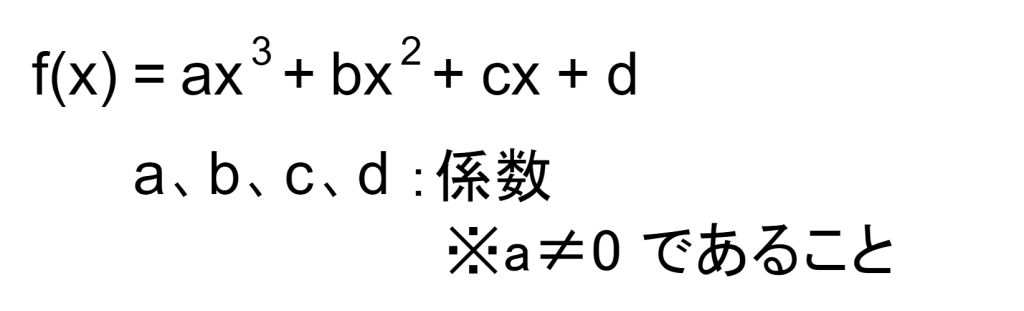
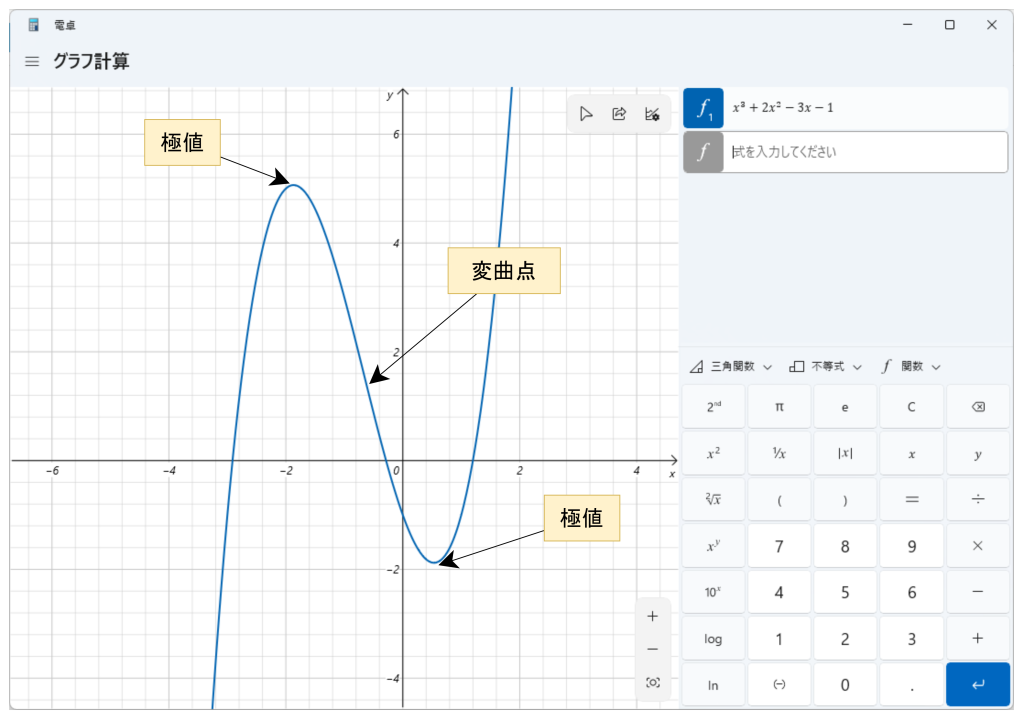
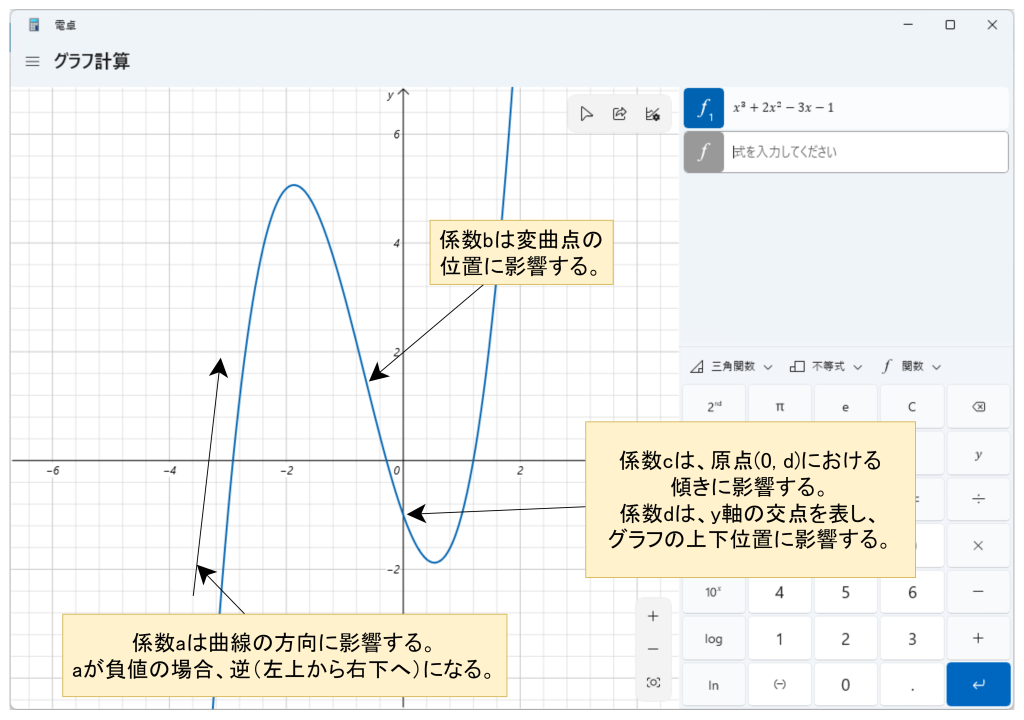
3次関数をグラフで表現するとS字曲線になります。その際、山と谷のそれぞれを極値といい、凸型から凹型に切り替わる点を変曲点と言います。

おわりに

AIを学び始めると、多項式関数のグラフを頻繁に目にすることになります。特に線形回帰などの機械学習では、多項式回帰が用いられることがあり、学習ではモデルの係数を推定します（次数はモデル設計で決定します）。また、近年のAI技術を代表するニューラルネットワークも、非線形変換を重ねることで多項式を含む複雑な関数を近似できる構造を持っています。実際には多次元の特徴量空間で計算しますが、機械学習の直感をつかむには、2次元の多項式関数で考えるだけでも十分です。

ちなみにWindows付属の電卓では、今回添付した画像の通りグラフを描くことができます。結構便利で、ネイピア数を使った曲線も描けるのでお勧めです。

ではまた。