AIを深く知りたい人のための数学 第3回 方程式の解き方

皆さん、こんにちは。LP開発グループのn-ozawanです。
来週金曜はハロウィンですね。ハロウィンと言えばカボチャ料理ですが、ハロウィン発祥の地であるアイルランドでは、コルカノンやボクスティなどのジャガイモ料理が主流なんだそうです。

本題です。
よく「○○の方程式」と言う言葉で、特定の現象や成功の秘訣、人生観などを“方程式”に例えて表現したりしますね。やはりシステム開発で方程式を解く機会はあまりありませんが、IT技術を支える基礎知識として理解する必要はあります。今回は中学数学で習う方程式です。

※「AIを深く知りたい人のための数学」は、数学を忘れてしまったエンジニアを対象に、中学数学から思い出すことを目的としたシリーズです。

方程式

例えば以下の式からxの値を求めます。xを求めるには、上記の式をx = ○○という形にすれば良いです。そのためにあれやこれやと工夫するのが方程式です。解き方は移項等ありますが、要は両辺に四則演算をしていくだけです。

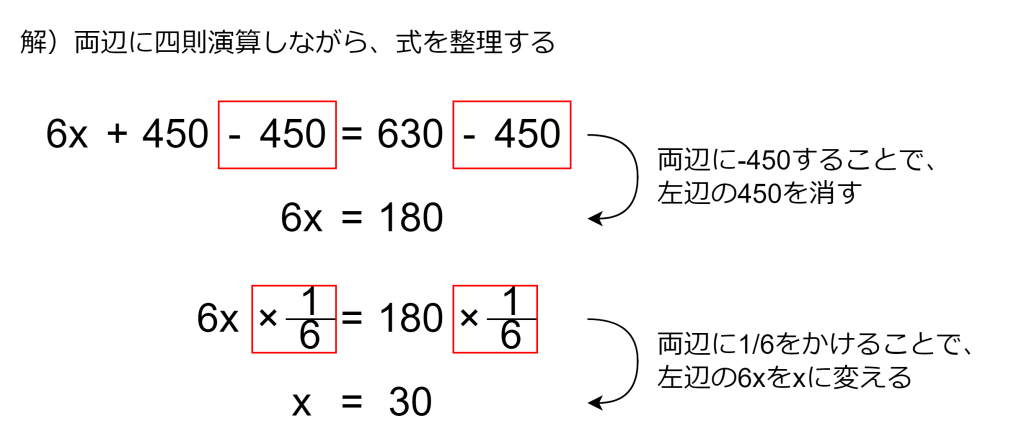
余談ですが、プログラム言語を初めて勉強すると必ず、「プログラムのx=○○は、数学のx=○○と意味が異なる」と習います。数学のx=○○は「xの値は○○である」という意味で、プログラムのx=○○は「変数xに○○を代入する」という意味になります。

連立方程式

例えば以下の式からxとyの値を求めます。先ほどの方程式同様、色々と工夫を凝らしてx = ○○とy = ○○という形にすれば良いです。解き方には加減法と代入法の二通りがあります。

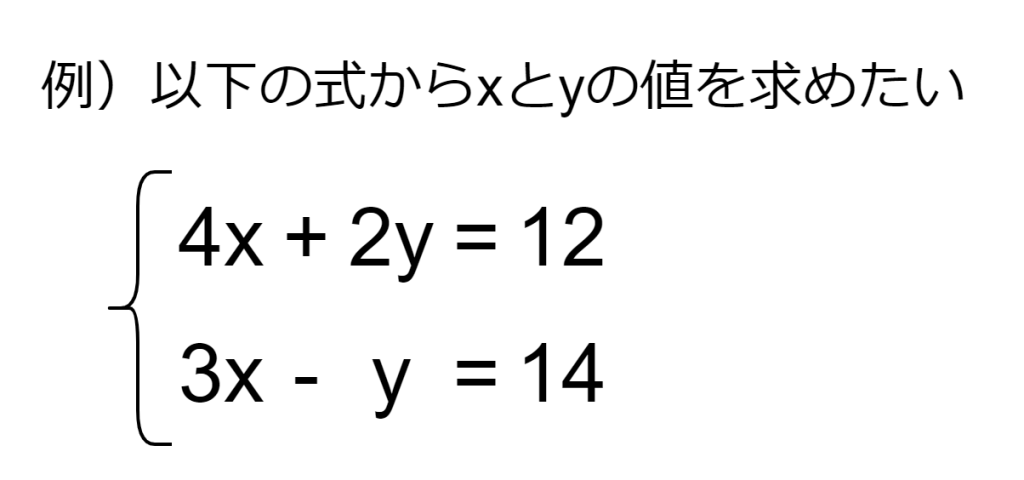
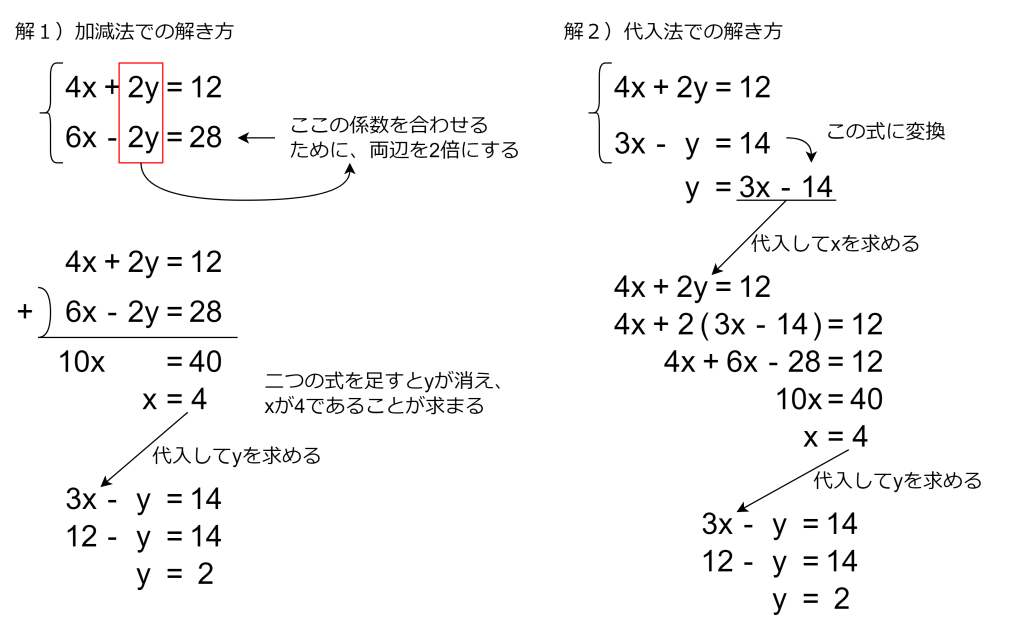
他にも線形代数を利用することで、よりシンプルに解くことができます。機械学習・AIでは大量の連立方程式を計算しており、線形代数を利用して効率よく計算しています。

2次方程式

例えば以下の式からxの値を求めます。「2次」とある通り、2次方程式はxの2乗を含む方程式を解きます。xの2乗を扱うので、答えに平方根が登場します。また、答えが2つになるのも2次方程式の特徴です。

なお、2次方程式の解の公式は以下になります。数学が苦手だと頭が痛くなりますね。

おわりに

今回、方程式をテーマに記載しましたが、非常に懐かしく感じました。方程式は数学の基礎知識ですので、もし忘れてしまった方はこの機会に思い出してみてください。

ではまた。