ソートや探索のアルゴリズムでよく見かける計算量オーダーって何?
皆さん、こんにちは。LP開発グループのn-ozawanです。
10月に入り一気に気温が下がりましたね。気温の変化は自律神経を乱し、体調不良を引き起こします。先ほどからくしゃみが止まりません。皆さんも体調管理には気を付けてください。
本題です。
アルゴリズムを学んでいると、「計算量はO(n)になります。」とか、「計算量はO(log n)となり、非常に高速です。」という文章を目にすることがあると思います。「Oってなんだ?」「logってなんだ?」という疑問が浮かぶものの、アルゴリズムの動きから効率の良さは理解できるので、深堀することなく結局分からずじまいということになっていませんか?今回はそんな計算量オーダーについてのお話です。
目次
計算量オーダー
計算量オーダーってなに?
計算量オーダーとは、とあるアルゴリズムがデータの入力数に対して、どれくらいの計算量を必要とするのかを表します。例えば線形探索は、配列の先頭から順に該当のデータを探します。ソースコードにすると以下になります。
public static int linearSearch(int[] array, int target) {
for (int i = 0; i < array.length; i++) {
if (array[i] == target) {
return i;
}
}
return -1;
}配列arrayの要素数分をfor文で繰り返して、見つかったらそのindex値を返却しています。その際、配列arrayの要素数が100個あれば最大100回繰り返すことになります。1億個あれば最大1億回繰り返すことになります。線形探索の計算量が、データの入力数(この場合は配列の要素数)に依存していることが分かると思います。この時、計算量オーダーは最大でO(n)と表現します。nは配列の要素数であり、配列の要素数に比例して計算量が増えるよ、という意味になります。
このように計算量オーダーは、アルゴリズムの効率性をざっくりと表す指標となります。特に入力数が増えたときに、どれぐらいの処理が必要となるのかが分かるようになります。例えば計算量オーダーがO(2n)であれば入力数の倍の処理が必要ですし、計算量オーダーがO(n2)であれば入力数が増えれば増えるほど処理が増大することが分かります。
良く使われる計算量オーダーは以下の通りです。
| 計算量 | 説明 | 例 |
|---|---|---|
| O(1) | 定数時間:入力数に関係なく一定時間である | 配列の1つの要素を取得 |
| O(n) | 線形時間:入力数に比例する | 配列を1回ループ |
| O(n2) | 二次時間:入力数の2乗に比例 | 配列を二重ループ |
| O(log n) | 対数時間:急速に減る | 二分探索 |
| O(n log n) | 線形対数時間:効率的なソート | マージソート、クイックソート |
| O(2n) | 指数時間:非常に遅い | 再帰的な全探索 |
ラウダウのO記法ってなに?
計算量オーダーは、「O」で表記されます。このOは、ラウダウのO記法と呼ばれています。OはアルファベットのOで、Ordnung(ドイツ語で整理や順序の意味らしいです)の頭文字に因みます。
ラウダウのO記法は、アルゴリズムや関数の漸近的な振る舞いを表すための記法です。この「漸近的な振る舞い」とは、ある値が限りなく大きくなった時の振る舞いを意味しています。計算量オーダーの場合、データの入力数が限りなく大きくなった時に、アルゴリズムや関数がどれぐらい計算量が増えるのかを表現しています。
logってなに?
計算量オーダーで良く出てくる「log」は、数学の対数です。とある数と底の関係から、その指数を求める関数です。計算量オーダーでは対数の底が省略されていますが、多くの場合は対数の底は2です。
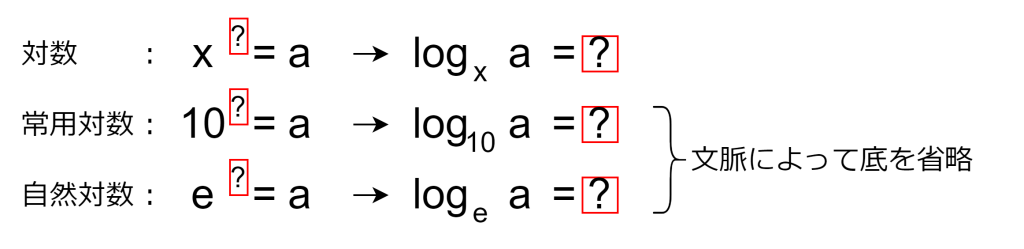
二分探索を例に
二分探索の計算量オーダーはO(log n)です。なぜ対数が使われるのでしょうか。
二分探索はソート済みの配列に対して、該当の値が中央値よりも低いのか高いのかで、探索する範囲を絞っていく手法です。
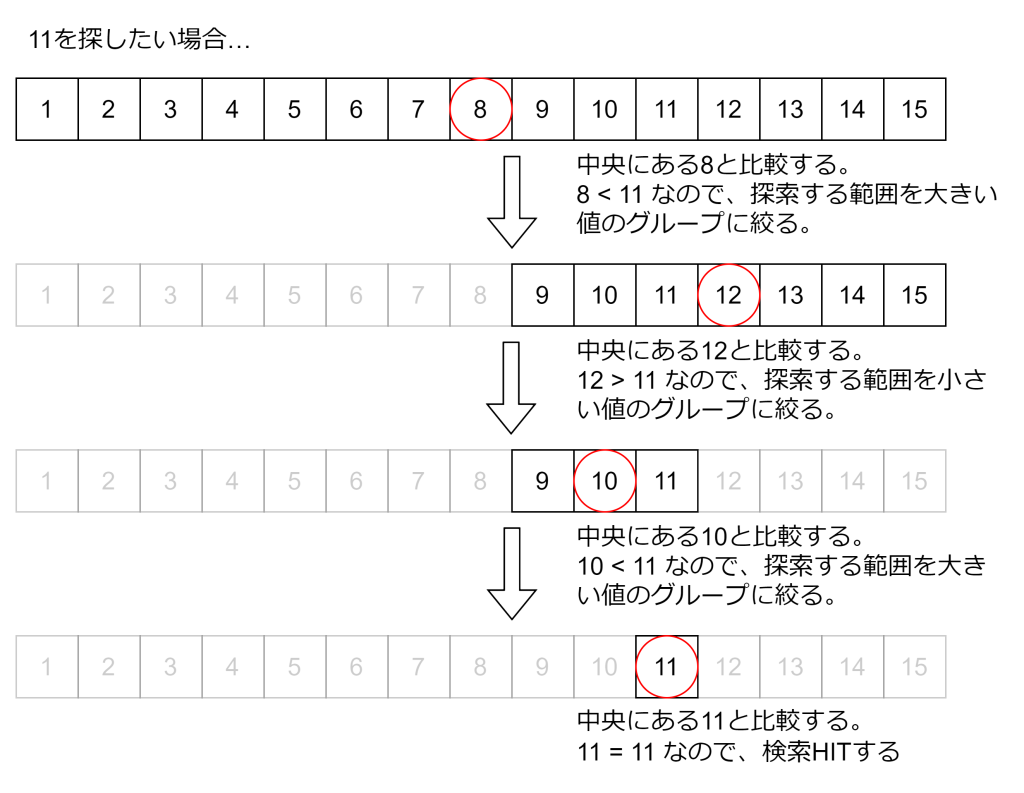
二分探索の特徴は探索する範囲が1/2に半減していくことです。この1/2になることが、計算量オーダーでlogが使われる理由になります。
累乗における指数法則に以下があります。同じ底同士で割る場合、指数同士を引きます。これは指数の数分、繰り返しaで割ると1になることを表しています。a5であれば、aを5回割れば1になります。
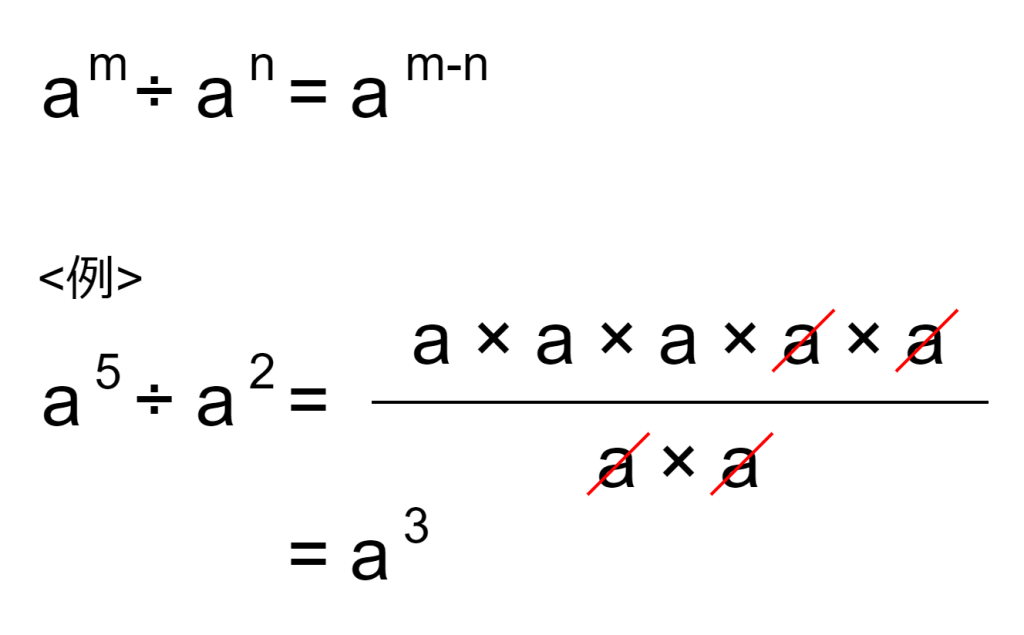
例えばデータの入力数nが16個であることを想定します。16は24で表すことができます。先ほども述べた通り、二分探索の特徴は探索する範囲が1/2に半減することです。つまり、24を4回繰り返し1/2にすれば、探索範囲は1つのみとなり、該当の値を見つけることができます。
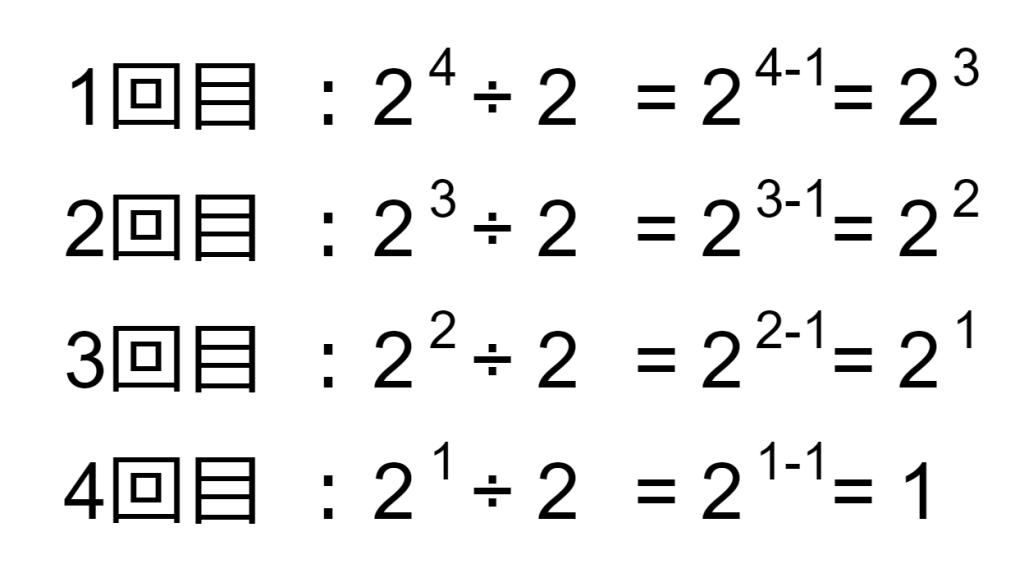
と言うことは、二分探索における繰り返しの回数は、データの入力数nと底が2のときの指数と言うことになります。つまり繰り返す回数はlog2 nと言うことになり、計算量オーダーはO(log n)となります。
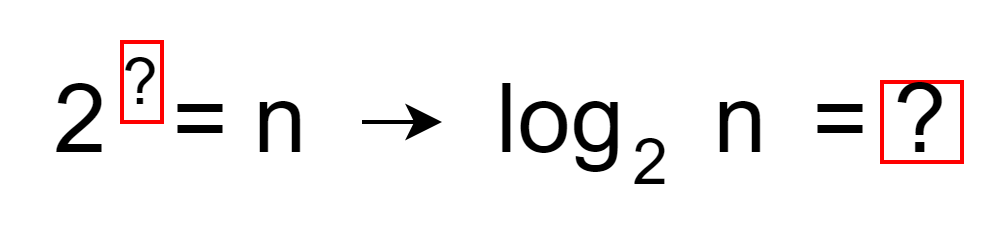
おわりに
計算量オーダーはあくまで計算量を表現するものであって、処理時間を表現するものではありません。と言うのも、処理時間はマシンの性能や通信速度などにも影響するからです。そういう意味では純粋にそのアルゴリズムの効率性を評価できる指標だと言えます。
ではまた。

 アイオス コーポレートブログ
アイオス コーポレートブログ
















