AIを深く知りたい人のための数学 第1回 数の種類

皆さん、こんにちは。LP開発グループのn-ozawanです。
麻酔は神経細胞の活動を抑制し、痛みの情報を脳に伝達するのを遮断します。そんな麻酔ですが、実は神経細胞が無い植物にも効果があり、麻酔を打たれた植物は動かなくなるそうです。

本題です。
このIT業界は理数系の分野だと思われていますが、実は数学の知識を必要とする機会はほとんどありません。生成AIの活用が広まってきていますが、効率よくAIに指示を与えるにはどうすればいいのかが主な題目であり、数学を使う機会はほぼないでしょう。しかしAIの仕組みを深く知ろうとしたとき、偏微分や総和、行列などの数学が出てきて面喰ってしまったエンジニアはいるのではないでしょうか。この「AIを深く知りたい人のための数学」では、そんな数学を忘れてしまったエンジニアを対象に、中学数学から数学を思い出すことを目的としたシリーズです。第１回は数の種類について整理します。

数の種類

はじめに

AI技術を学ぶために数の種類を整理する必要はないかもしれません。ただ、数の種類を整理することは、数学を学び直すにあたってちょうどいい題材になるかと思います。

整数と小数

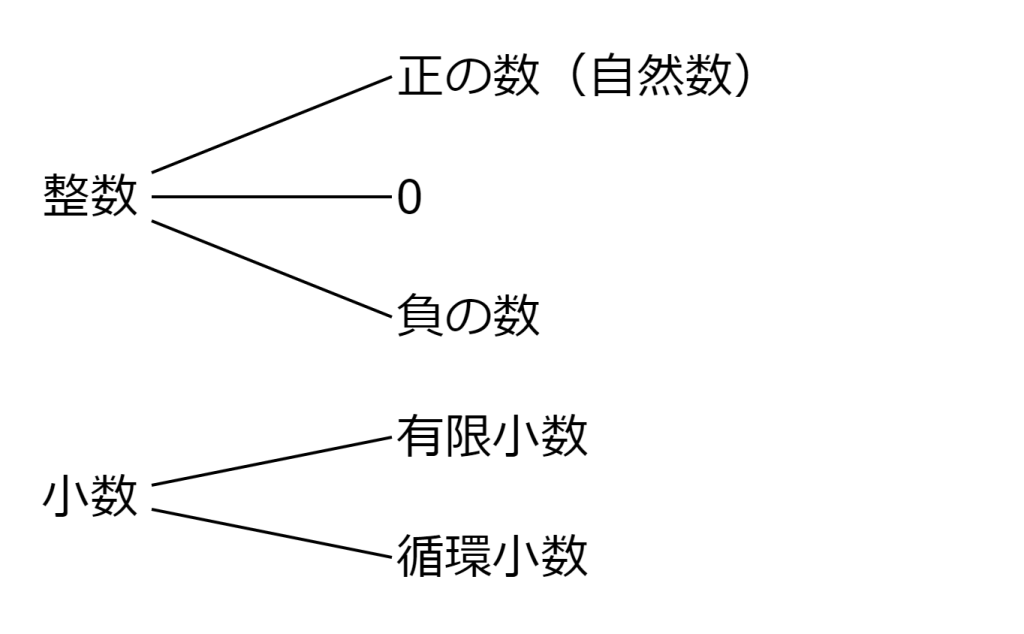
整数とは小数や分数を含まない数（…-3、-2、-1、0、1、2、3…）のことです。整数は更に正の数（自然数）、0、負の数に分類されます。また、整数と小数にはその特性からいくつか分類があります。

偶数と奇数

2で割り切れる数字（2、4、6…）を偶数、2で割り切れない数字（1、3、5…）を奇数と呼びます。

ちなみに0は2で割り切れるため偶数です。2で割り切れる数字が偶数であるということは、任意の整数(k)を2倍したときに、その結果(n)は偶数であることを指します。任意の整数(k)に0を指定するとその結果は0となりますので、0は偶数となります。

素数と合成数

1と自身の数以外に割り切れる数を持たないものを素数（2、3、5、7…）と呼びます。素数以外を合成数と呼びます。2025年10月現在、発見された素数の最大値は 2^136279841 – 1 で、41,024,320桁もあるのだそうです。全然イメージ付きませんね。

素数は暗号化技術で重要な役割を果たします。詳細な説明は省きますが、大きな素数同士で掛け合わせた大きな数は、素因数分解が困難である性質があります。特に公開鍵暗号方式であるRSAの暗号鍵は、この性質を利用しており、昨今の暗号化技術の安全性を担保しています。

有限小数と循環小数

小数の内、小数点以下が有限の桁数で終わる小数を有限小数（0.75、2.5）、同じ数字の繰り返しが続く小数を循環小数（0.333…、1.232323…）と呼びます。

余談ですが、コンピュータの世界では数値を2進数で扱うため、小数を浮動小数点として表現します。その為、小数を正確に表現することができない場合があり、例えば以下のコードだと誤動作になる可能性があります。プログラムする際は小数を考慮して実装する必要があります。

#include <stdio.h>

void main() {
  if (0.1 + 0.2 == 0.3) {
    printf("True\n");
  } else {
    printf("False\n");   // こっちが処理される
  }
}

有理数と無理数

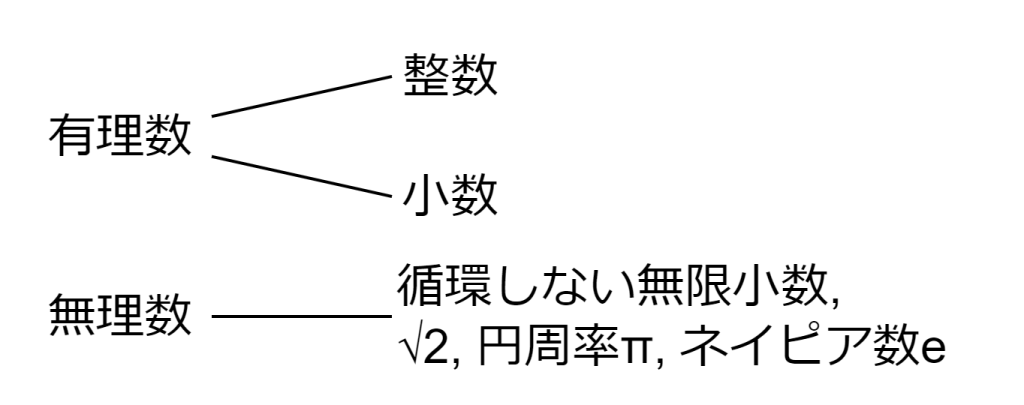
整数と小数は整数同士の比（分数）で表現することができ、これを有理数と言います。一方で分数で表現することができない数を無理数と言います。無理数には√2や円周率π、AIを勉強すると必ず出てくるネイピア数eがあります。ネイピア数eに関しては、また別の記事で話題にしたいと思います。

実数と虚数

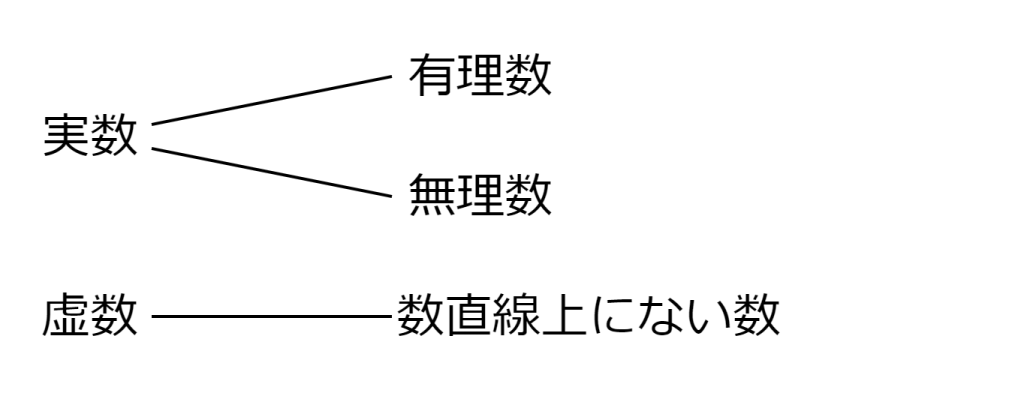
これまで登場した数はすべて数直線上で表すことができ、これらすべてを実数と呼びます。

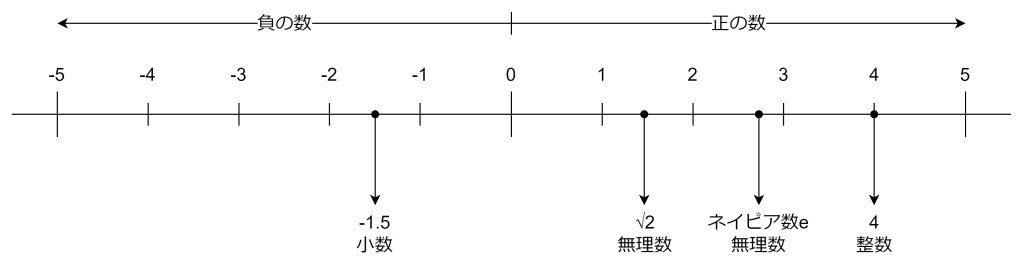
一方で数直線上に表されない数を虚数と呼びます。例えば、i² = -1 のような式があった場合、このiに該当する値は数直線上に存在しません。このようなiのことを虚数と呼びます。

おわりに

虚数は難しいですね。イメージができないため難しく感じます。調べてみると、量子コンピュータや画像処理におけるフーリエ変換、複素数ニューラルネットワークなるものもあり、虚数は昨今のIT技術でも活躍しているようです。もう少し勉強して、いずれ複素数と虚数で記事を書きたいです。

ではまた。