バッチ勾配降下法、確率的勾配降下法、ミニバッチ勾配降下法

皆さん、こんにちは。LP開発グループのn-ozawanです。
ジブラルタル海峡はヨーロッパ大陸とアフリカ大陸を隔てる海峡で、最も狭いところでは14キロメートルとなります。これは東京湾アクアラインの15キロメートルよりも短い距離となります。

本題です。
勾配降下法は、損失関数の値を最小化するために、重みやバイアス項を少しずつ調整していく最適化手法です。詳細は前回の投稿をご確認ください。そんな勾配降下法ですが、学習データを1件ずつ取り込んで調整するのか、まとめて取り込んで調整するのかで、いくつかの手法が存在します。今回はバッチ勾配降下法、確率的勾配降下法、ミニバッチ勾配降下法を取り上げたいと思います。

勾配降下法

バッチ勾配降下法

バッチ勾配降下法は、学習データ全体を一度に使ってパラメータを更新する手法です。例えば学習データが1000件ある場合、1000件すべてを順伝搬で予測して、1000件分の平均損失から勾配を求め、勾配降下法で各層の重みやバイアス項の係数を調整します。

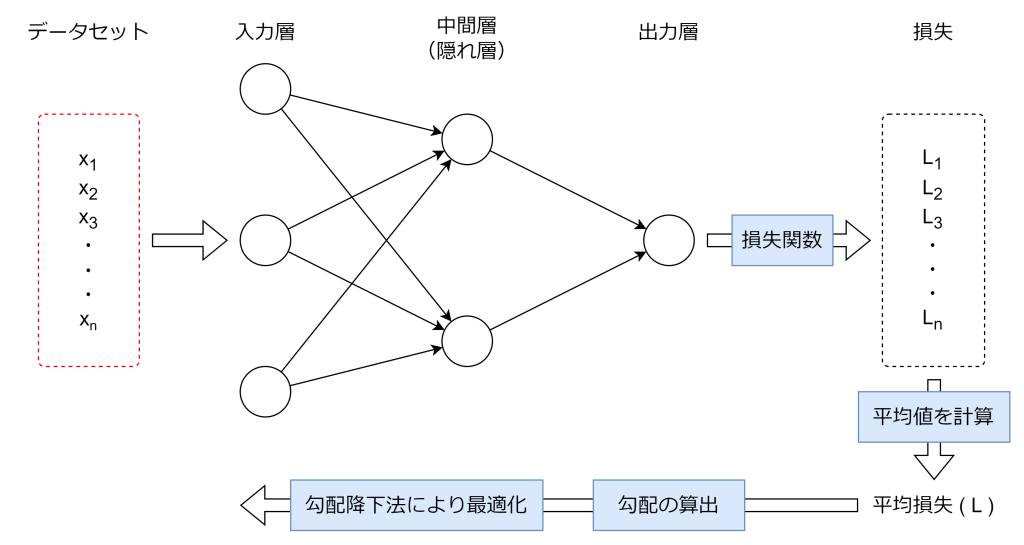
この方法では、学習データ全体の情報を反映した更新が行われるため、学習が安定して収束（損失やパラメータの変化が十分小さくなった状態のこと）しやすくなります。しかし、学習データが大規模になると、すべてのデータを毎回計算する必要があるため、計算コストやメモリ消費が大きくなりやすいです。例えば、数百万件のデータを持つ場合、1回のパラメータ更新に非常に多くの時間がかかることがあります。

バッチ勾配降下法は学習データが少ない場合や、計算資源に余裕がある場合に適した手法です。全データを使うことで安定した学習が可能ですが、データ量が多い場合は他の手法も検討する必要があります。

確率的勾配降下法

確率的勾配降下法は、学習データの中から1つをランダムに選び、そのデータだけを使ってパラメータを更新する手法です。選ぶと言うと少々語弊があるかもしれません。実際には学習データをシャッフルして1件ずつ学習します。例えば学習データが1000件ある場合、その1000件をシャッフルして、1件ずつ順伝搬で予測して、その損失から勾配を求め、勾配降下法で各層の重みやバイアス項の係数を調整します。

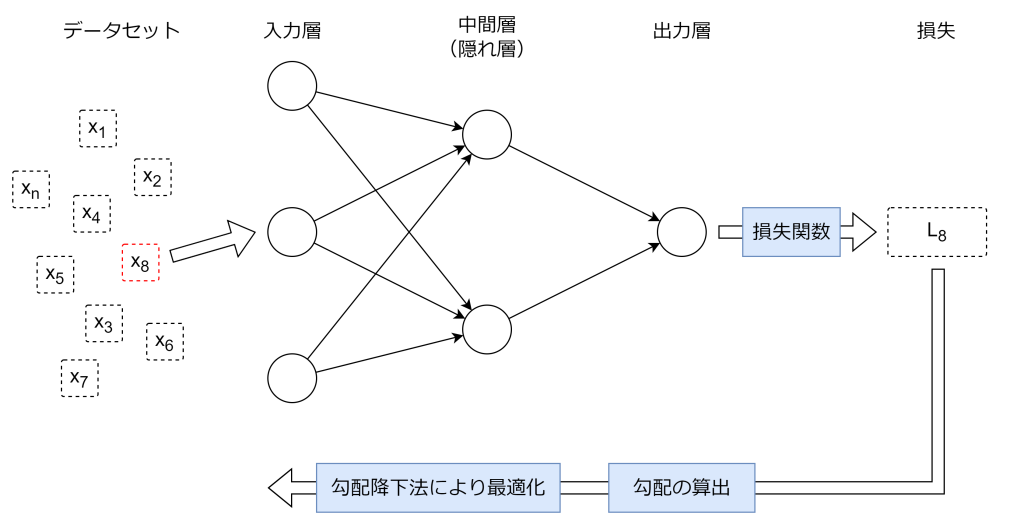
学習データ全体を使うバッチ勾配降下法と比べて、1回の更新ごとに必要な計算量が大幅に少なくなりますが、データのノイズや外れ値などにより、損失関数の値や勾配の推定にばらつきが生じやすく、モデルが不安定になりやすくなります。

確率的勾配降下法は学習データが多い場合や、計算資源が限られている場合に有効な手法です。ただし、更新ごとのばらつきが大きいため、学習率の調整が非常に重要になります。

ミニバッチ勾配降下法

ミニバッチ勾配降下法は、学習データを複数の小さなグループ（ミニバッチ）に分割し、それぞれのミニバッチごとにパラメータを更新する手法です。学習データ全体を使うバッチ勾配降下法と、1つのサンプルのみを使う確率的勾配降下法の中間的な方法といえます。

例えば学習データが1000個ある場合、1回の学習で32個や64個など、決められた数のデータをまとめてミニバッチとして扱います。各ミニバッチごとに損失関数の平均や勾配を計算し、その結果を使ってパラメータを更新します。これにより、計算コストと勾配推定の安定性のバランスを取ることができます。

ミニバッチ勾配降下法は、学習データが多い場合でも計算資源を有効に使いながら、安定した学習を実現できる手法です。ミニバッチのサイズは、計算環境やデータの特性に応じて適切に選択することが重要です。

おわりに

バッチ勾配降下法は安定した学習が可能ですが、データ量が多い場合は計算コストが高くなりやすいです。一方で確率的勾配降下法は低い計算コストで学習が可能ですが、データのノイズや外れ値などに影響を受けやすく、思い通りに学習が進まなくなるリスクがあります。ミニバッチ勾配降下法はバッチ勾配降下法と確率的勾配降下法のいいところ取りで、一番バランスよく学習が行えるため、多くの場合ではミニバッチ勾配降下法が採用されるそうです。

ではまた。