誤差逆伝搬法からの勾配降下法 (ニューラルネットワーク)

皆さん、こんにちは。LP開発グループのn-ozawanです。
地球は自転による遠心力により楕円体となっています。その為、海抜標高ではエベレストが世界一ですが、地球の中心からの距離であればチンボラソがエベレストよりも高くなります。この理屈で言うと、日本で一番高い（地球の中心から最も離れている）地点は、富士山ではなく沖ノ鳥島になります。

本題です。
以前、主に多層構造となるニューラルネットワークの学習方法について整理しました。学習には損失関数、誤差逆伝搬法、勾配降下法の３つポイントがあります。今回はその内の１つである勾配降下法を深堀したいと思います。

勾配降下法

概要

勾配降下法は、損失関数の値を最小化するために、重みやバイアス項を少しずつ調整していく最適化手法です。具体的には、誤差逆伝搬法により求めた損失関数の勾配（偏微分）から、その勾配の反対方向に重みとバイアス項を更新します。

実際の計算式では、勾配は「損失が最も増える方向」を示しますので、その逆方向に更新することで損失を減らしていきます。

wは各層の重みやバイアス項です。ηは学習率で次項で扱います。Lは損失です。図でイメージすると以下のようになります。wが勾配分の移動を繰り返すことにより、徐々に勾配が0になる個所を探し出します。

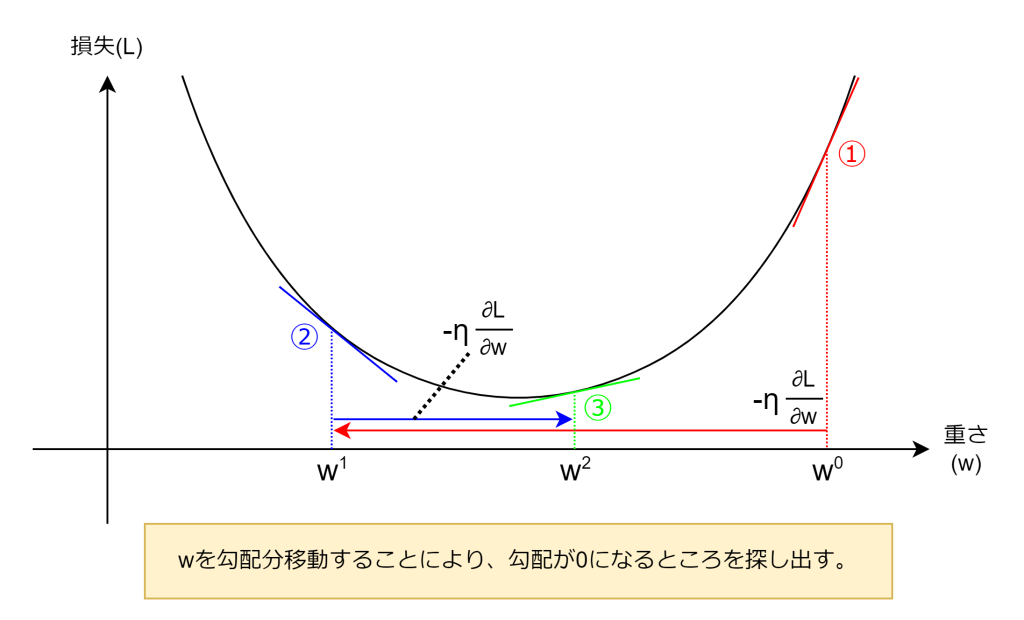
学習率

学習率はハイパーパラメータで、勾配に沿って一度にどれだけ降りていくかを決定するパラメータになります。学習率は安定かつ効率的に学習するために用いられます。

例えば、ニューラルネットワークの最初の各層の重みやバイアス項は未学習の状態ですので、その値はまだ最適化されていません。なので、勾配が急だったり緩やかだったりします。もし、学習率を使わなかった場合、各層の重みやバイアス項が更新幅が安定しなくなりうまく学習が進みません。そこで学習率によって調整するのです。

ただし、学習率の調整には注意が必要です。学習率が大きすぎても小さすぎても、いつまでたっても収束（損失やパラメータの変化が十分小さくなった状態のこと）せず、学習が完了しません。

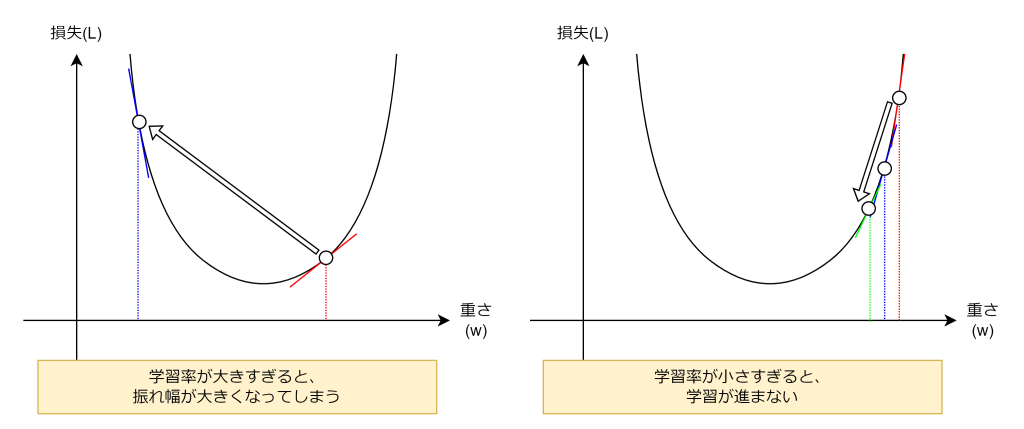
局所最適解と鞍点

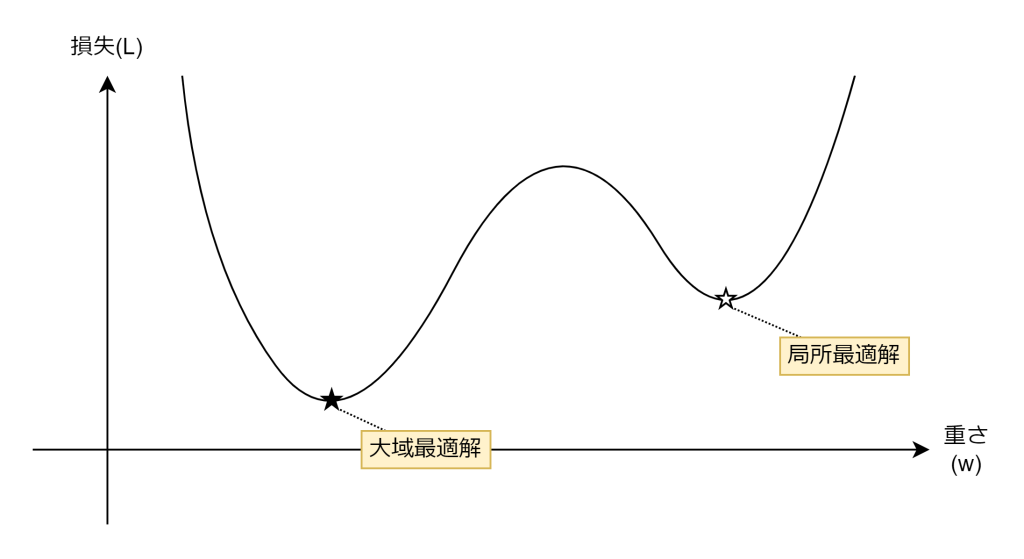
探索する関数が綺麗なU字型の関数とは限りません。以下のような関数の場合、勾配が0になる個所が2つ存在します。☆が局所最適解であり、★が大域最適解と呼び、学習においては損失が最も少ない大域最適解を探し出す必要があります。

勾配降下法は少しずつ勾配の逆方向に調整するだけの手法ですので、自身がいる場所が局所最適解なのか大域最適解なのか判断できません。局所最適解に一度陥ると、なかなか抜け出すのが困難となります。

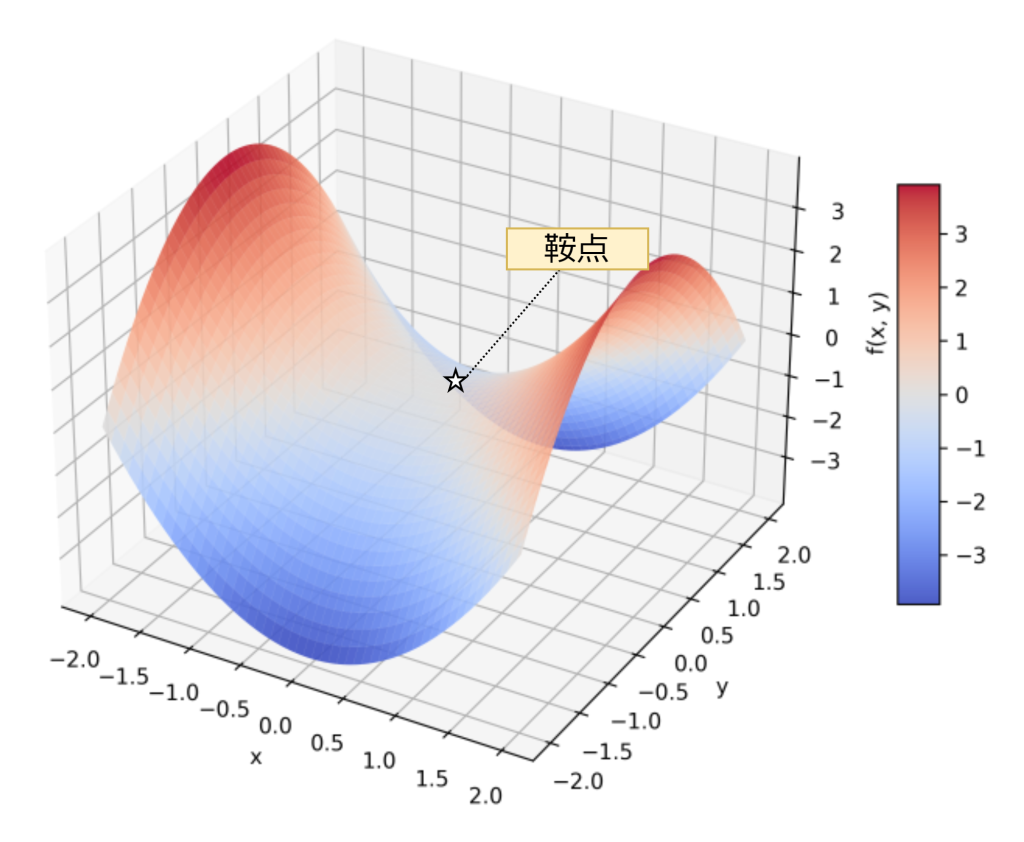
また、3次元以上ではより厄介なことに、鞍点と呼ばれる、ある次元から見れば極小であるものの、別の次元から見ると極大となってしまう点が存在します。この鞍点も一度陥ると、なかなか抜け出すのが困難となってしまいます。

これら局所最適解や鞍点などの対策として、学習率を調整して強引に抜け出すことが挙げられます。それ以外にも、モーメンタムやAdam、AdaBoundと言った手法で解決することができます。

おわりに

正確には勾配降下法ではなく、どちらかと言うと誤差逆伝搬法の問題ではありますが、勾配が消失する勾配消失問題と、勾配が増加する勾配爆発問題があります。どちらもネットワークの深さや活性化関数の性質、各層の重さやバイアス項が不適切などの要因が重なり起きる問題で、この問題が発生すると勾配による最適解の探索ができなくなり、学習が失敗する原因になります。

ディープラーニングは1980年代に提唱されましたが、1990年代に下火となってしまいました。その原因はコンピュータの演算能力が不足していたこともありましたが、勾配消失問題により多層にしても学習精度が向上しない問題が立ちふさがったためです。この問題に対して活性化関数の工夫や、各層の重さの初期値を適切に設定するXavierなどの手法が登場したことにより、第3次AIブームが起きて昨今のAI技術に繋がったと言われています。

ではまた。