誤差逆伝搬法を理解したい

n-ozawan

2025.09.03

AI G検定対策機械学習

皆さん、こんにちは。LP開発グループのn-ozawanです。
ハチドリは空中で静止するために、毎秒約55回も羽ばたいており、全動物中で最も活発な代謝を行っています。加えて、体が極めて小さいことで放散も激しいため、常に花の蜜からカロリーを摂取しないとすぐに餓死するのだそうです。

本題です。
以前、主に多層構造となるニューラルネットワークの学習方法について整理しました。学習には損失関数、誤差逆伝搬法、勾配降下法の３つポイントがあります。今回はその内の１つである誤差逆伝搬法を深堀したいと思います。

誤差逆伝搬法

概要

誤差逆伝搬法は、ニューラルネットワークの学習において、出力結果と正解ラベルとの差（損失）をもとに、各パラメータがどれだけ損失に寄与しているかを計算します。誤差逆伝搬法の名前の由来は、出力層から入力層で遡って伝搬して計算するところに因んでいます。

誤差逆伝搬法の目的は、各層の重みやバイアス項が損失関数にどれだけ影響を与えているのか、損失関数の勾配を求めることにあります。勾配が求まると、各層の重みやバイアス項が変化したときに、損失がどれぐらい変化するのか、その変化量が分かるようになります。その変化量は、損失が減る方向に対して各層の重みやバイアス項をどれぐらい調整すればいいのかの指針になります。

チェーンルール

誤差逆伝搬法はチェーンルールの応用で計算を行います。

チェーンルールは、複数の関数が入れ子になっている場合に、全体の微分を効率よく計算するための方法です。例えば、以下のように関数が入れ子になっているとします。

y = f (g (x))

この関数が入れ子となっている式に対してyをxで微分するとき、まず内側の関数 g(x) の微分を求め、その結果に外側の関数 f の微分を掛け合わせます。これにより、複雑な関数の微分も段階的に計算できます。

\frac{∂y}{∂x} = f ‘ (g (x)) \times g ‘ (x)

誤差逆伝搬法では、各層の勾配を計算する際に、各層の出力が次の層の入力となるため、局所的な微分を掛け合わせて全体の勾配を求めます。その為、チェーンルールに基づいて計算する必要があるのです。

計算式

では、実際にどういう計算を行うのかを見てみましょう。誤差逆伝搬法の計算式は、各層のパラメータに対する損失関数の勾配を求めることにあります。具体的には、出力層から入力層に向かって、各層の重みやバイアスに対する微分値を計算します。計算式は以下の通りです。

Lは損失です。yは活性化関数の結果で、出力層であれば予測結果になります。zは総和で線形変換の結果で、活性化関数に入る前の値になります。wは各層の重みやバイアス項です。

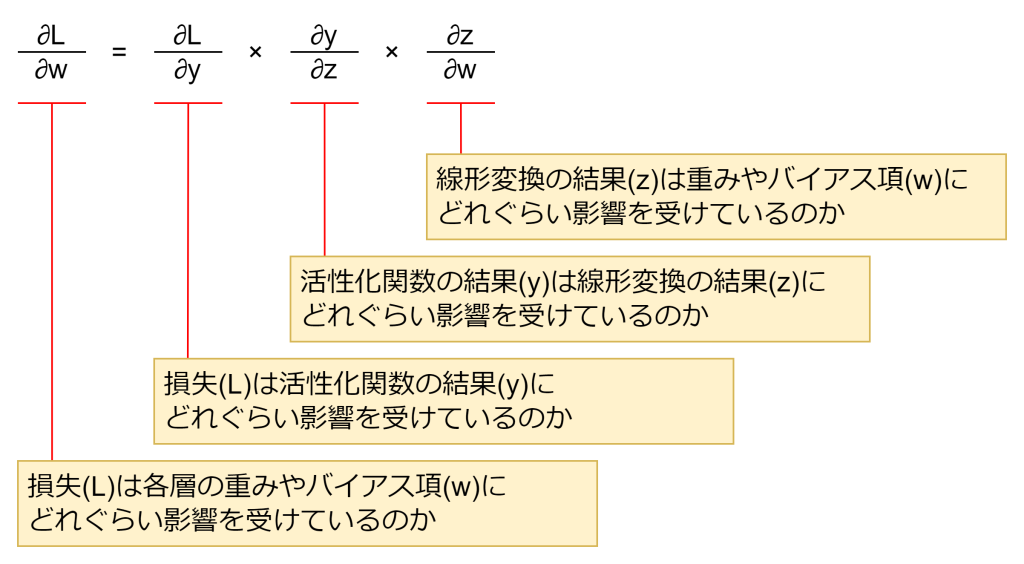
日本語でこの式を表現すると、先ほども言った通り、誤差逆伝搬法は「各層の重みやバイアス項(w)が、どれぐらい損失(L)に影響するのか」を求めます。つまり、∂L / ∂w です。

この各層の重みやバイアス項(w)から損失(L)への道程には、いくつかの要因があります。まず、損失(L)は活性化関数の結果(y)に影響されます（∂L / ∂y）。そして、活性化関数の結果(y)は線形変換の結果(z)に影響されます（∂y / ∂z）。最後に、線形変換の結果(z)は重みやバイアス項(w)に影響されます（∂z / ∂w）。この数珠繋ぎにより上記の計算式となる訳です。