正則化で過学習を抑制する

n-ozawan

2025.08.27

AI G検定対策機械学習

皆さん、こんにちは。LP開発グループのn-ozawanです。
一部のクラゲでは、ポリプ期と呼ばれる岩や海底などに付着して生活した後、成体クラゲに成長します。ベニクラゲは成体クラゲからポリプ期まで退行する（若返る）ことができるため、不老不死のクラゲで有名です。

本題です。
前回、前々回で損失関数を取り上げました。機械学習ではこの損失Lを最小化するように重みなどの係数を調整することで学習を行います。その際に気を付けなければならないのは過学習です。今回は過学習を抑制する正則化に関するお話です。

正則化

概要

正則化は、機械学習モデルの過学習を防ぐための手法です。特にディープラーニングはモデルの表現力が高いため、何も考えずに学習すると過学習の影響を大きく受けてしまいます。過学習についてはこちらを参照ください。

有名な正則化手法には「L1正則化」と「L2正則化」があります。これら正則化は損失関数にペナルティを課すことで過学習を防ぎ、よりシンプルで汎化性能の高いモデルを作ることを目的としています。

L1正則化

L1正則化は、損失に係数の絶対値和を加える手法です。数式は以下の通りです。

J (x) = L + λ \sum_{i = 1}^{n} | w_{i} |

Lは損失です。Lに加えているのがL1正則化であり、損失に対して課すペナルティになります。λは正則化の強さでハイパーパラメータです。w_iは重みになります。例えばニューラルネットワークの場合、各ニューラルへの重みの絶対値和を損失Lに加算します。

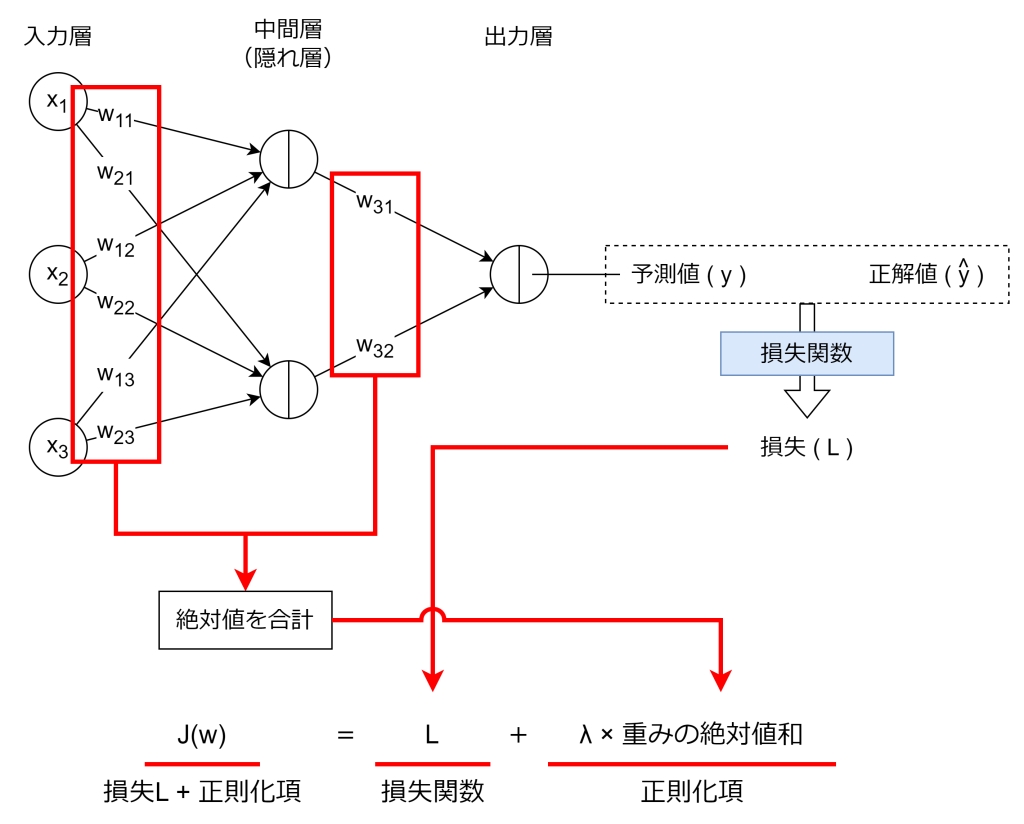
L1正則化は、スパース性と呼ばれる、あまり出力結果に寄与しない特徴量があれば、その重み(w_i)を0にする性質があります。これにより計算コストを減らし、よりシンプルなモデルにすることができます。その反面、あまりやりすぎると必要な特徴量の重みまで0になってしまい、精度が下がります。ハイパーパラメータのλを調整することで、適切に重みを最適化します。

L2正則化

L2正則化は、係数の二乗和を損失に加える手法です。数式は次の通りです。

J (w) = L + λ \sum_{i = 1}^{n} {w_{i}}^{2}

Lは損失関数の値です。Lに加えているのがL2正則化であり、損失に対して課すペナルティになります。λは正則化の強さでハイパーパラメータです。w_iは重みになります。例えばニューラルネットワークの場合、各ニューラルへの重みの2乗和を損失Lに加算します。

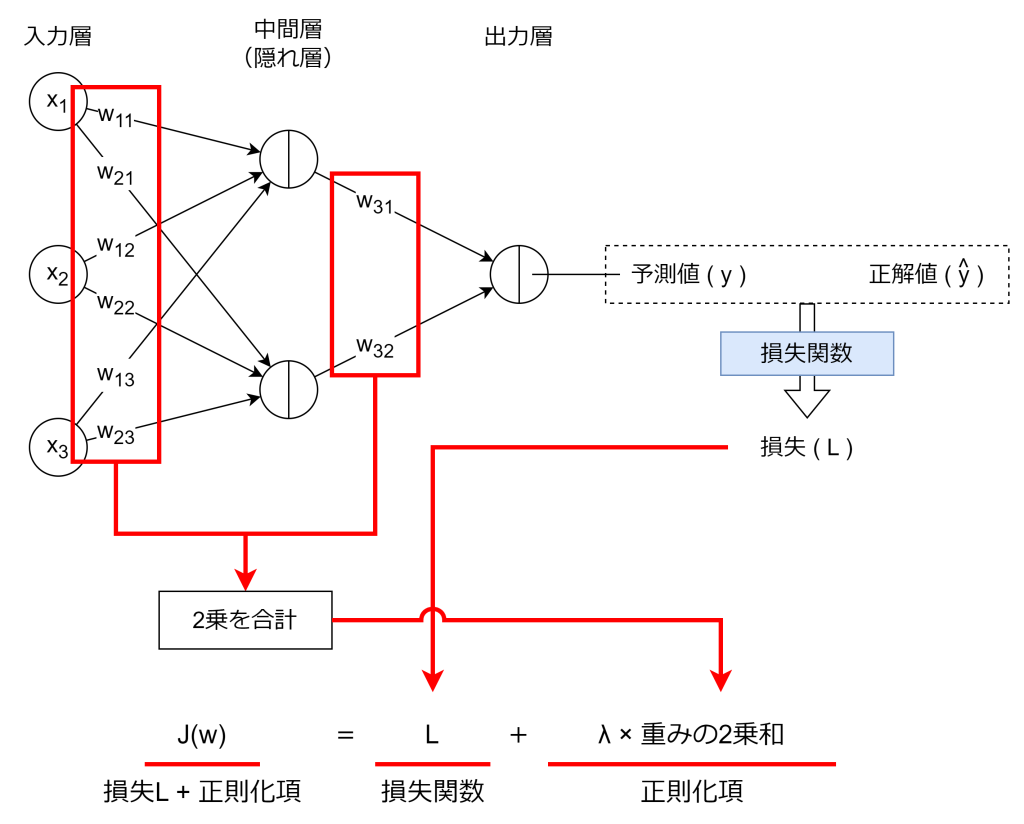
L1正則化と比べて、L2正則化にスパース性はありません。その反面、重み全体を均等に縮小させる性質があり、ノイズや誤情報に強く、L1正則化と比べて過学習を防ぎやすくなります。

Elastic Net

L1正則化とL2正則化を組み合わせた手法として、Elastic Netがあります。数式は次の通りです。

J (w) = L + λ \sum_{i = 1}^{n} | w_{i} | + λ \sum_{i = 1}^{n} {w_{i}}^{2}

損失Lに、L1正則化とL2正則化を加算しています。

おわりに

過剰に適合しようと複雑なモデルが構築されると、学習データのノイズや偶然のパターンまで思えてしまう、いわゆる過学習が起きます。また、機械学習における重みなどの係数は、その値が大きければ大きいほど出力結果に強く影響してしまい、モデルが不安定になる要因にもなります。L1正則化とL2正則化は、モデルをシンプルに、重みなどの係数を小さくすることで過学習を防ぐことができます。

ではまた。