損失関数（主に交差エントロピー誤差）を学ぶ

皆さん、こんにちは。LP開発グループのn-ozawanです。
強い乾燥はDNAの損壊を引き起こします。クマムシ等の生物は乾燥状態でも生き延びる耐性があり、DNA損壊への強い防御機能もしくは修復機能を持っています。その結果、地球上では過剰ともいえる放射線耐性も併せ持つようになったと考えられています。

本題です。
前回は主に多層構造となるニューラルネットワークの学習方法について整理しました。学習には損失関数、誤差逆伝搬法、勾配降下法の３つポイントがあります。今回はその内の１つである損失関数を深堀したいと思います。

損失関数（誤差関数）

損失関数（誤差関数とも言います）は、順伝搬から算出された予測値と正解値との誤差を数値化します。誤差が大きいということは、その分、予測から大きく外れているということになります。統計学などの分野では予測が外れることは「コスト」や「損失」と捉えることもあり、誤差のことを損失とも言います。

損失関数は多くの関数があります。今回は有名どころの平均二乗誤差と交差エントロピー誤差を取り上げます。実際はその機械学習の用途や目的等から最適な損失関数を選ぶことになります。

平均二乗誤差

平均二乗誤差（MSE）は、主に回帰問題で利用され、回帰モデルの予測値と実測値との差（残差）を二乗し、その平均を求めたものです。平均二乗誤差は以下の式で表されます。

詳細は「回帰問題の機械学習モデルを性能評価する方法」で取り上げていますので、そちらを参照してください。

交差エントロピー誤差

交差エントロピー誤差は、主に分類問題で利用される損失関数です。モデルの予測と正解の確率分布がどれぐらい異なるのかを数値化します。特に多値分類や確率的な出力を持つモデルで広く用いられています。交差エントロピー誤差は以下の式で表されます。

上記式のp(x)は正解の確率分布で、q(x)は予測した確率分布です。このlogは自然対数（底がe）になります。p(x)とq(x)の確率分布が似ていると損失は小さくなり、異なっていると損失は大きくなります。実際に計算してみましょう。

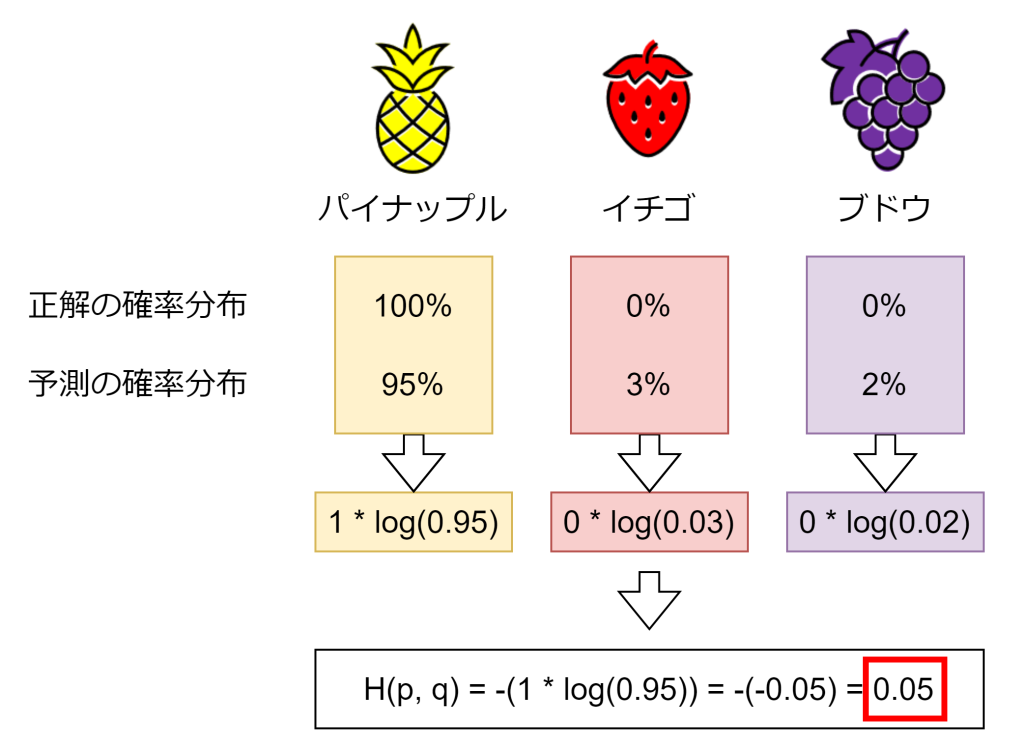
例えば、果物の画像をパイナップル、イチゴ、ブドウのいずれかに識別するAIを考えます。パイナップルの画像を示された場合、正解の確率分布pは(1.0, 0, 0)となります。識別した結果、予測の確率分布qが(0.95, 0.03, 0.02)で高い精度の場合、交差エントロピー誤差は「0.05」になります。

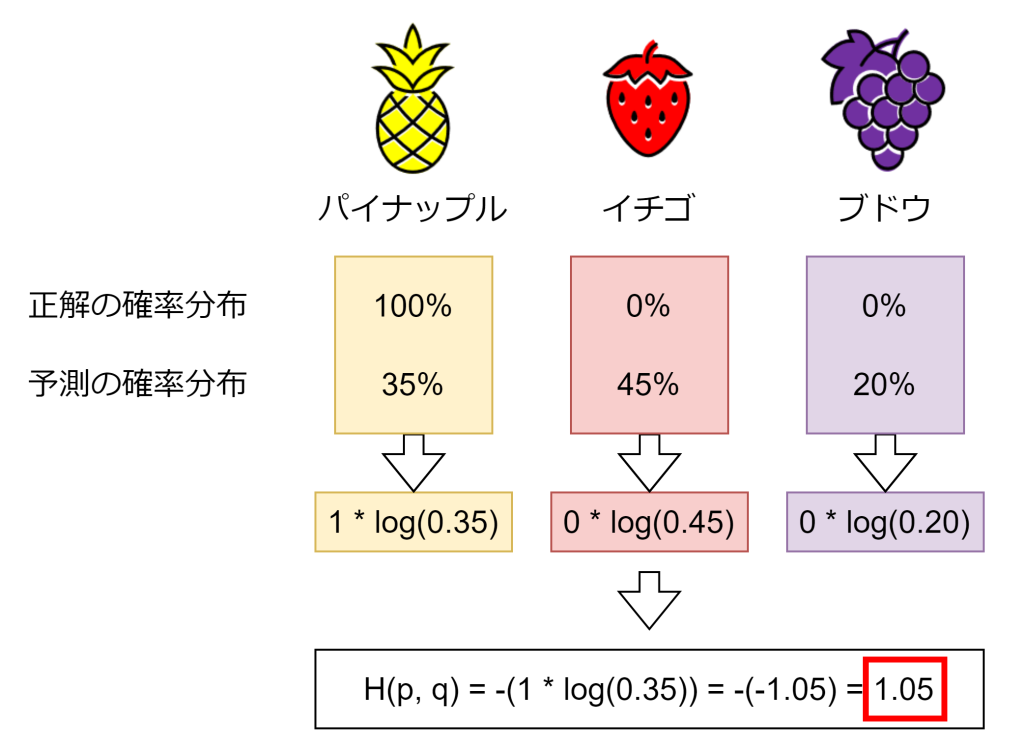
もう一つ例を出します。今度は予測の確率分布qが(0.35, 0.45, 0.20)で低い精度の場合、交差エントロピー誤差は「1.05」になります。先ほどの高い精度で得られた0.05と比べ、より大きな数値（損失）が得られました。

おわりに

損失関数として代表的な平均二乗誤差と交差エントロピー誤差を挙げましたが、先ほども述べた通り、損失関数は多くあります。例えば、回帰問題であれば平均絶対誤差やHuber損失がありますし、確率分布のズレを測る指標としてカルバック・ライブラー情報量などがあります。その機械学習の用途や目的などに合わせて使い分けることが重要です。

ではまた。