ニューラルネットワーク～多層パーセプトロンを理解する～

n-ozawan

2025.08.06

AI G検定対策分類分析機械学習

皆さん、こんにちは。LP開発グループのn-ozawanです。
8月ですね。日本では記録的な猛暑が続きますが、南半球のオーストラリアでは記録的な大雪になっているとか。ちなみに気象庁のHPには、世界の異常気象をまとめたページがあります。

本題です。
昨今のAI技術の中核をなすディープラーニングを理解するために、その基礎となるニューラルネットワークを勉強中です。前回は単純パーセプトロンを取り上げましたので、今回は少し発展させた多層パーセプトロンを勉強したいと思います。

ニューラルネットワーク

単純パーセプトロン（前回のおさらい）

前回のおさらいです。ニューラルネットワークは、人間の脳の神経回路を模倣した機械学習モデルです。単純パーセプトロンは、入力層と出力層のみの、最も単純な構造をしたニューラルネットワークです。

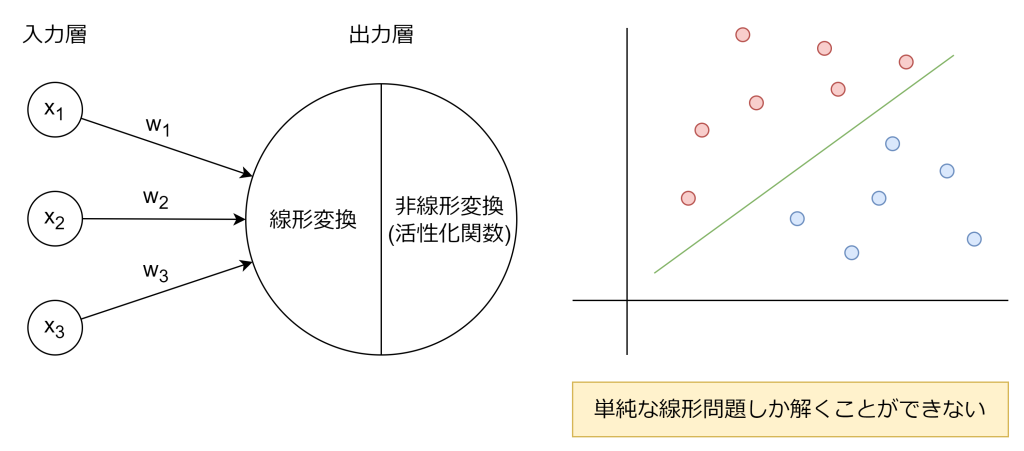
ニューロン（ノードとも呼びます）では、線形変換と活性化関数による非線形変換の2段階の処理が行われます。単純パーセプトロンはそのシンプルな構造のため、単純な線形問題しか解くことができません。

多層パーセプトロン

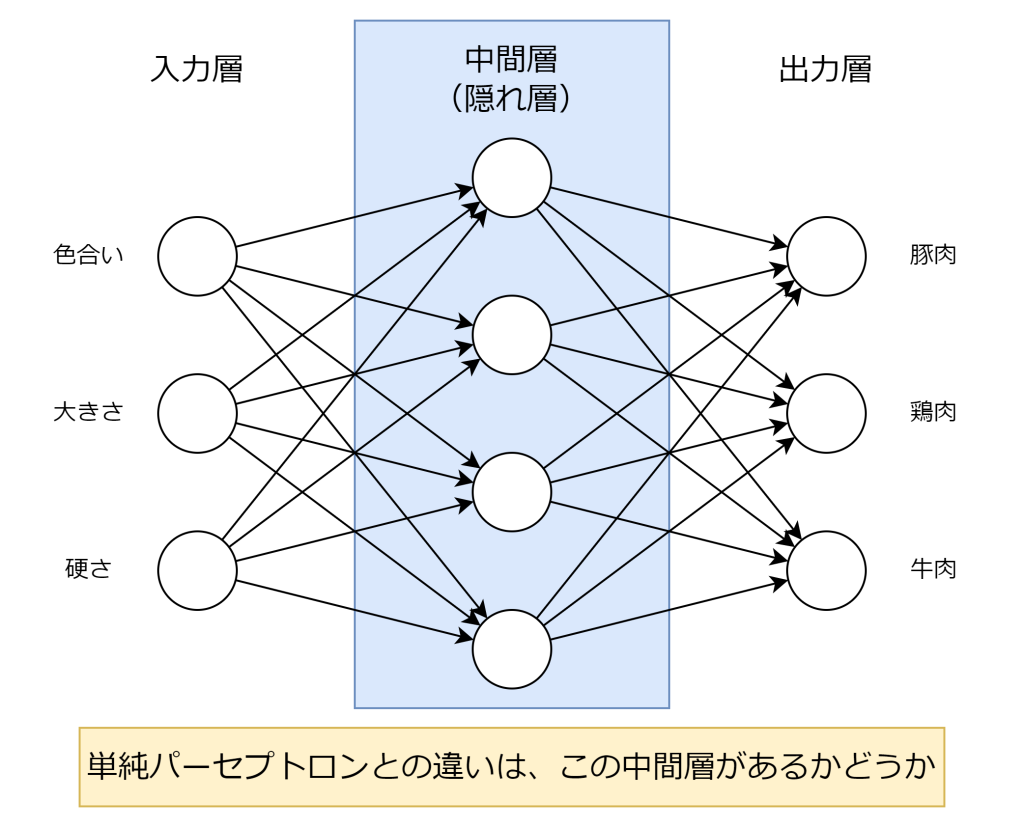
多層パーセプトロンは、入力層と出力層の間に１つ以上の中間層（隠れ層とも言います）が存在するニューラルネットワークです。各層のニューロンは前の層の全てのニューロンと接続されており、単純パーセプトロンと同様に線形変換と活性化関数による非線形変換を繰り返します。

線形変換は単純パーセプトロンと同じで、入力値（x_i）に対して重み（w_i）をかけて足し合わせたものになります。具体的には以下の式で求めます。

z = \sum_{i = 1}^{n} x_{i} w_{i} + b

非線形変換で使用する活性化関数はシグモイド関数やソフトマックス関数、ReLU関数などが使用されます。単純パーセプトロンで使用したステップ関数はあまり使用しないようです。シグモイド関数は、必ず0から1までの値を返す関数で、以前、ロジスティック回帰の時でも登場しました。

σ (z) = \frac{1}{1 + e^{- x}}

多層パーセプトロンは、単純パーセプトロンでは解けなかった非線形な問題も扱えるようになります。これは、中間層を通じて入力データの特徴をより複雑に変換できるためです。

計算してみる

実際に計算してみましょう。活性化関数は中間層と出力層、ともにシグモイド関数を使用します。入力値（x_i）と重み（w_i）、バイアス項（b）は以下の通りです。計算をシンプルにするため、出力層は1つにします。

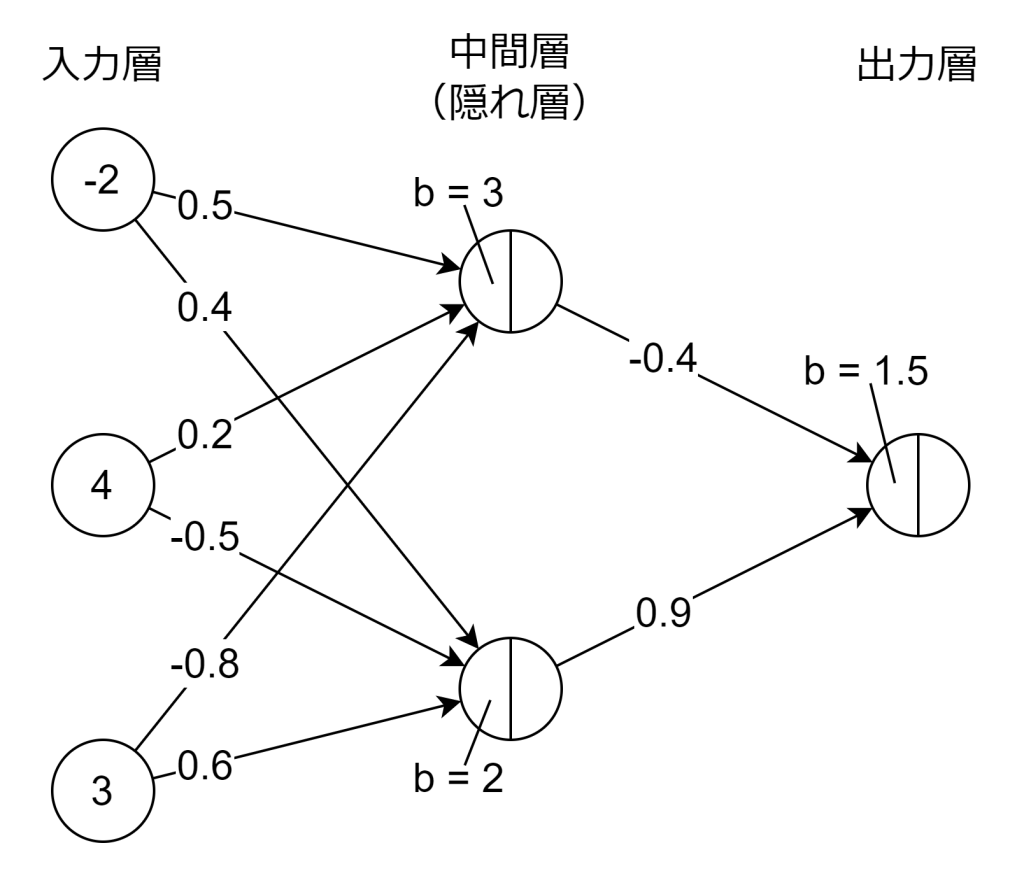
1つ目の中間層を計算します。計算結果は以下の通りです。

線形変換により0.4という数字が得られ、その0.4をシグモイド関数で計算すると0.5987という数字が得られました。

では次に2つ目の中間層を計算します。計算結果は以下の通りです。

線形変換により1.0という数字が得られ、その1.0をシグモイド関数で計算すると0.7311という数字が得られました。

では最後に出力層を計算します。計算結果は以下の通りです。