ニューラルネットワーク ～単純パーセプトロンから理解する～

皆さん、こんにちは。LP開発グループのn-ozawanです。
土曜の丑の日にウナギを食べる習慣は、江戸時代の平賀源内が、旬から外れたウナギを売るためのキャッチコピーとして考案したのが始まりです。まさか絶滅危惧種に指定されてもなお食べ続けられるとは、当人たちも想像できなかったでしょうね。

本題です。
昨今の AI 技術の中核をなす機械学習と言えばディープラーニング（深層学習）でしょう。ディープラーニングを理解することは、昨今の AI 技術を理解することに繋がります。ディープラーニングは、ニューラルネットワークを更に発展させた機械学習です。まずは、シンプルな単純パーセプトロンから勉強したいと思います。

ニューラルネットワーク

概要

ニューラルネットワークは、人間の脳の神経回路を模倣した機械学習モデルで教師あり学習の一種です。主に分類問題に使われるアルゴリズムになります。

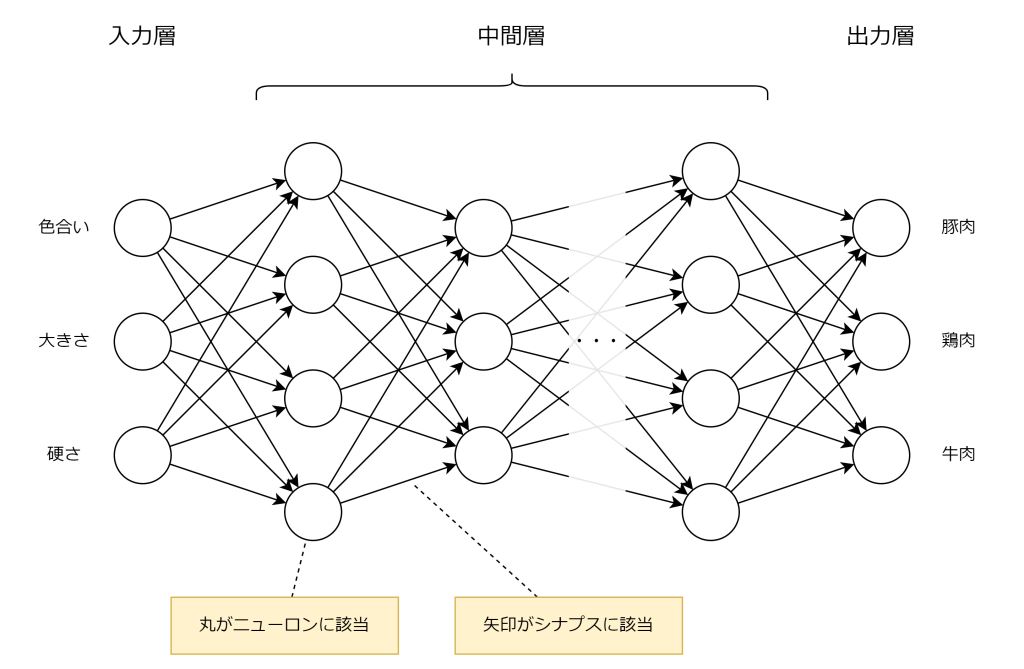
人間の脳には約 1000 億個の神経細胞（ニューロン）が存在し、これらが複雑に接続されて情報を伝達・処理しています。各ニューロンは他のニューロンとシナプスと呼ばれる接合部でつながり、電気信号や化学物質を介して情報をやり取りする高度なネットワークを形成します。この仕組みにより、脳は外部からの刺激を受け取り、学習や記憶、判断などを実現しています。この高度なネットワークを模倣したのがニューラルネットワークです。

以下はニューラルネットワークのイメージ図です。左の入力層から値を受け取り、中間層から出力層にかけて計算を行い、出力層にて結果を出力します。

線形変換と非線形変換

ニューロン（ノードとも呼びます）では、線形変換と非線形変換の2段階の処理が行われます。

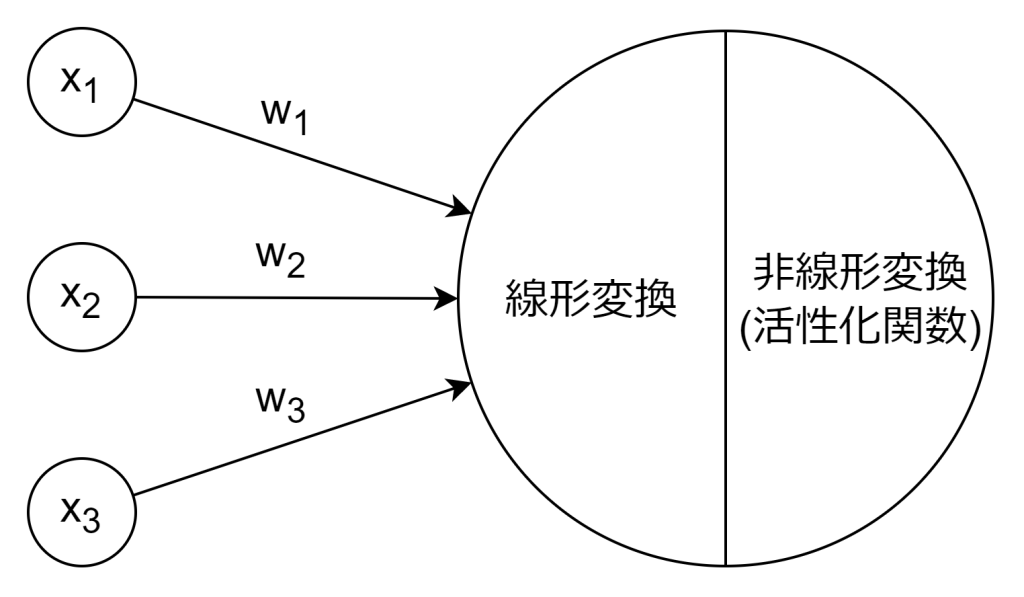
線形変換とは、入力値（x_i）に対して重み（w_i）を掛けて足し合わせる処理のことを指します。これは、入力ベクトルと重みベクトルの内積にバイアス項（b）を加える操作であり、数式で表すと以下のようになります。この処理だけでは、入力と出力の関係は直線的（線形）であり、複雑なパターンや非線形な関係を学習することができません。

$$z=\sum _{i=1}^n{x}_i{w}_i+b$$

一方、非線形変換は、線形変換の結果に活性化関数（例：ステップ関数、シグモイド関数、ReLU など）を適用することで実現されます。これにより、モデルはより複雑なパターンや非線形な境界を学習できるようになります。ニューラルネットワークが高い表現力を持つのは、この非線形変換を層ごとに繰り返し適用するためです。

単純パーセプトロン

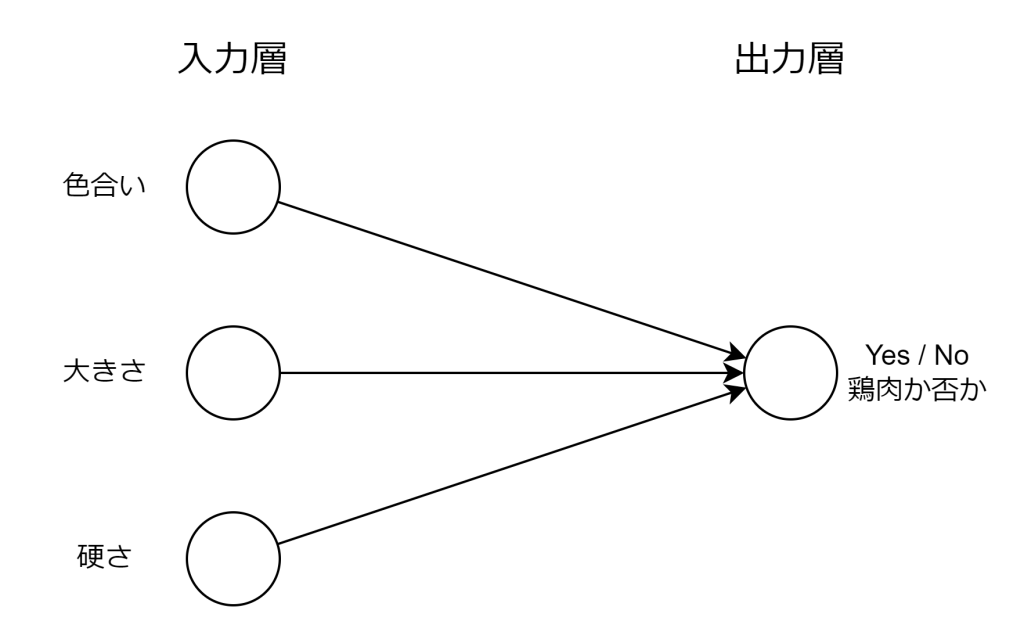
単純パーセプトロンは、1958 年に提案された最も基本的な人工ニューラルネットワークのモデルです。複数の入力層と1つの出力層のみの非常に単純な構成となっています。

ステップ関数

単純パーセプトロンの活性化関数ではステップ関数が使われます。ステップ関数は、入力の合計がある閾値を超えた場合に 1、そうでない場合に 0 を出力するものです。閾値を0とした場合の数式を表すと以下のようになります。

$$y=\{\begin{array}{cc}1& \text{if} x\ge 0\\ 0& \text{if} x<0\end{array}$$

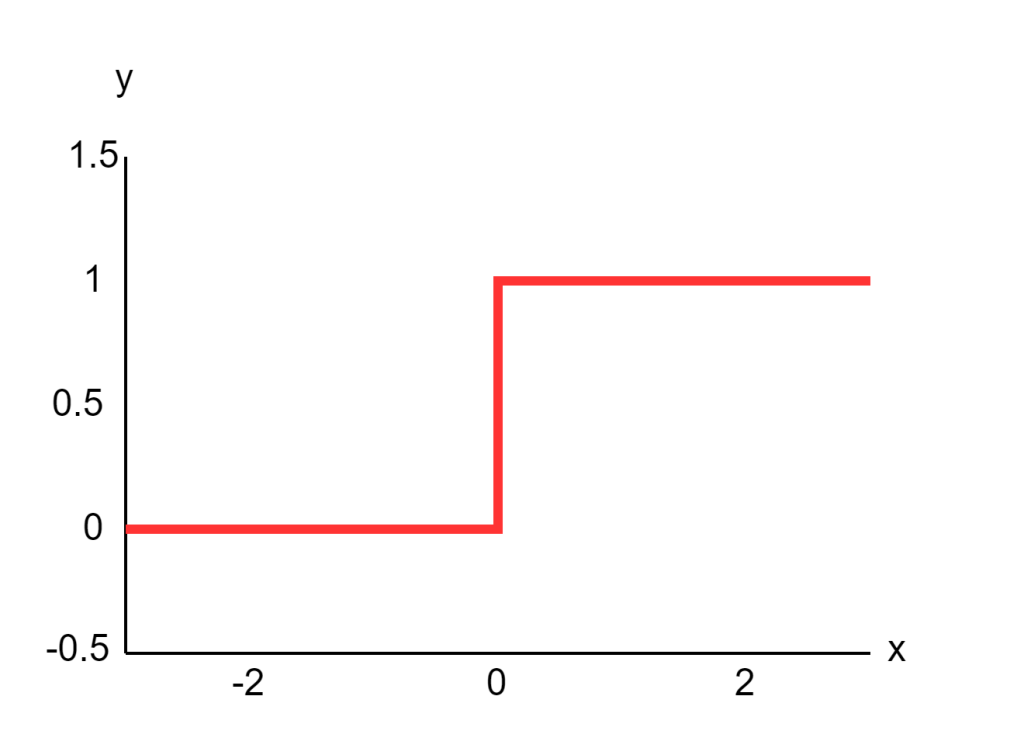
この関数により、単純パーセプトロンは入力を 2 つのクラスに分類することができます。なお、現代のニューラルネットワークでは、シグモイド関数や ReLU 関数など、より滑らかな活性化関数が使われることが多いです。

計算してみる

実際に計算してみましょう。入力値（x_i）と重み（w_i）は以下の通りです。バイアス（b）は3とします。

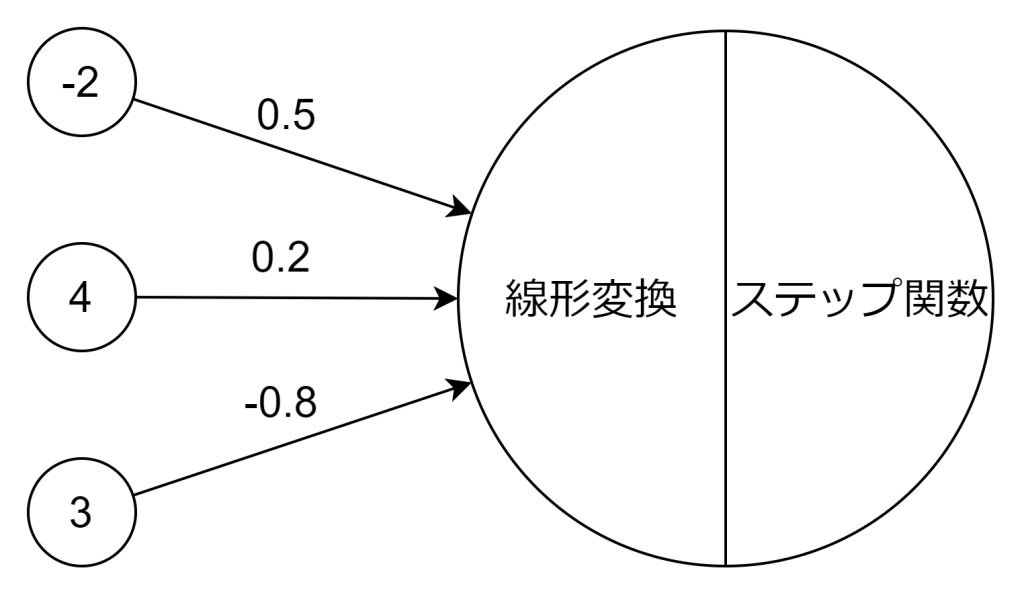
線形変換は以下のようになります。

$z=(-2\times 0.5)+(4\times 0.2)+(3\times -0.8)+3=-1.0+0.8-2.4+3=0.4$

z = 0.4となりました。この結果をステップ関数に渡すと、0を超えているので、1を返却します。よって、結果は1となります。

おわりに

単純パーセプトロンは単純な線形問題（YesかNoか）ぐらいしか解くことができないため、ニューラルネットワークの研究は下火になってしまいます。ディープラーニングの第一歩として単純パーセプトロンを見ましたが、これが何故、昨今のすごいAI技術になるのか、まったくイメージが湧きませんね。

ではまた。