主成分分析で特徴量を要約しよう
皆さん、こんにちは。LP開発グループのn-ozawanです。
北海道で史上初の40度に達するという予報が出ています。北海道の歴代最低気温は1902年1月25日に旭川市で観測された-41.0度なので、もし40度となった場合、その差は81度になります。
本題です。
例えばAIが、その画像が犬かどうかを判断する時、どこを見て判断するのでしょうか。顔の形、目の配置、鼻の高さ、毛並み等、多くの特徴を捉えながら判断します。この特徴が多ければ多いほど、計算量は増大します。中には足の数などのように、あまり関係ない特徴もあるかもしれません。そういった不要な特徴を削減したいときに主成分分析を用います。今回はそんな主成分分析のお話です。
目次
主成分分析
概要
主成分分析(PCA)は、多数の特徴量を持つデータに対して、情報の損失を最小限に抑えつつ、より少ない特徴量を作り出すことにより、少ない次元に変換する手法です。これにより、データの可視化やノイズ除去、機械学習モデルの精度向上などに役立ちます。
特徴量と次元
概要にて説明のあった「特徴量」と「次元」とは何でしょうか。
特徴量とは、データが持つ属性や性質を数値やカテゴリとして表現したものです。例えば、果物のデータには「重さ」「形」「色」「糖度」「硬さ」などの属性や性質があります。これらが果物の特徴量となります。
次元とは、数学的には空間の軸の数です。機械学習や統計の文脈では、特徴量の数がそのまま次元数になります。先ほどの果物であれば、特徴量は5つですので、5次元になります。
一般的に、2次元はX軸とY軸のグラフで表現され、3次元はX軸とY軸とZ軸のグラフで表現されます。しかし、4次元以上となるとグラフなどで視覚的に表現することが困難です。もちろん、次元が増えれば増えるほど計算量が大きくなります。現実世界では1つのデータを表現するには、多数の特徴量が必要になります。主成分分析は新しい特徴量を生み出すことで、次元を削減することが目的となります。
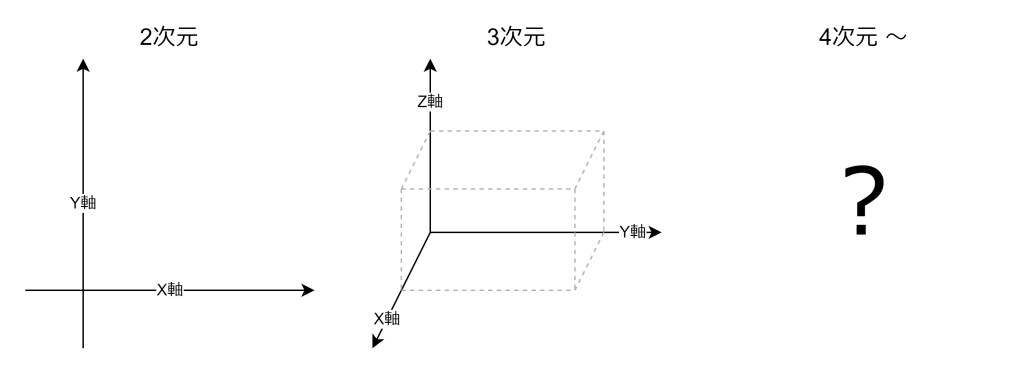
基本的な考え方
固有値
固有値とは、主成分(新しい特徴量)が元のデータの分散(情報量)をどれだけ説明しているかを示す指標です。固有値が大きいほど、その主成分がデータの特徴をよく表していることになります。
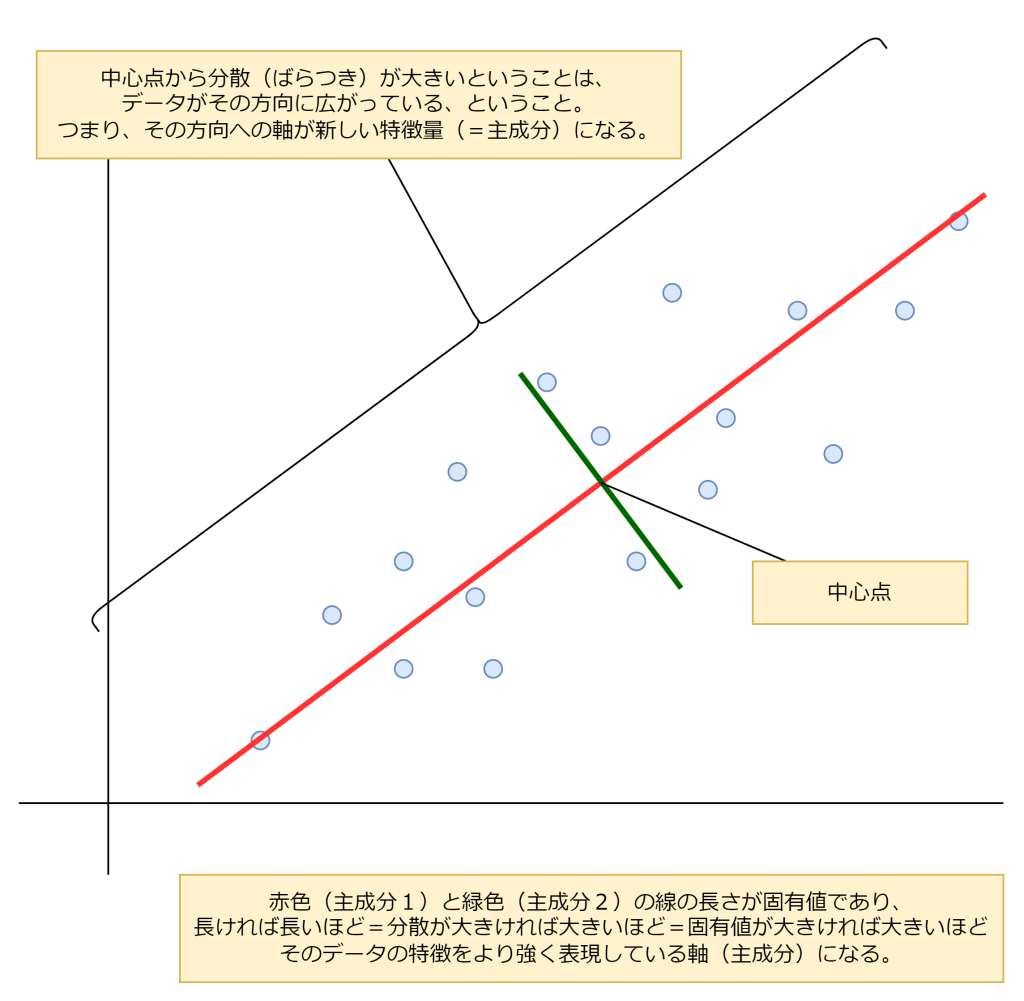
寄与率
寄与率とは、0から1までの数値で、各主成分が元のデータの分散(情報量)のうち、どれだけの割合を説明しているかを示す指標です。具体的には、各主成分の固有値を全ての固有値の合計で割ることで算出されます。寄与率が高い主成分ほど、データの特徴をよく表しているといえます。
累積寄与率
累積寄与率とは、上位から順に選択した主成分が元のデータの分散(情報量)のうち、どれだけの割合を説明しているかを累積で示す指標です。例えば、第一主成分と第二主成分の寄与率を合計した値が累積寄与率となります。累積寄与率が高いほど、選択した主成分で元のデータの情報を十分に表現できていることになります。一般的には、累積寄与率が80%や90%を超える主成分数を選択して次元削減を行います。
下の表は4つの主成分とそれぞれの固有値、寄与率です。主成分1と2の寄与率の合計(累積寄与率)は0.9で90%となります。よって、この主成分1と2でデータの特徴量を良く表現していることとなり、主成分3と4を削除することができます。
| 主成分 | 固有値 | 寄与率 |
|---|---|---|
| 1 | 67 | 0.54 |
| 2 | 45 | 0.36 |
| 3 | 8 | 0.07 |
| 4 | 4 | 0.03 |
おわりに
主成分分析は特徴量の次元削減によって、モデルの学習効率や精度を向上されるほか、多数の特徴量を2次元のグラフで表現することができるようになるため、マーケティング分野などで活用されているようです。
ではまた。

 アイオス コーポレートブログ
アイオス コーポレートブログ



















