回帰問題の機械学習モデルを性能評価する方法

皆さん、こんにちは。LP開発グループのn-ozawanです。
梅雨の時期によく見かけるカタツムリは、気温が低くなると冬眠します。梅雨の時期しか見かけないので、カタツムリは短命かと思っていたのですが、個体差はあるものの、10年以上も生きる個体もいるとか。

本題です。
前回は分類問題における性能評価を取り上げました。分類問題は想定通りに分類されたか否かであり、正解／不正解がはっきりしていますので、評価しやすいかと思います。では、回帰問題ではどのように性能を評価するのでしょうか。今回は回帰問題における機械学習モデルの性能評価についてのお話です。

モデルの性能評価

概要

回帰問題における機械学習モデルの性能評価は、主に予測値と実際の値との誤差を測定することで行います。分類問題では正解率やF値など「正しく分類できたか」を評価指標としますが、回帰問題では連続値の予測精度が重要となるため、誤差の大きさや分布に着目します。

代表的な評価指標として、平均二乗誤差（MSE）、二乗平均平方根誤差（RMSE）、平均絶対値誤差（MAE）などがあります。これらは予測値と実測値の差をさまざまな方法で集約し、モデルの予測性能を定量的に比較するために用いられます。回帰モデルの選択や改善の際には、これらの指標を参考にしてモデルの精度を評価します。

平均二乗誤差 (MSE)

平均二乗誤差（Mean Squared Error, MSE）は、回帰モデルの予測値と実測値との差（残差）を二乗し、その平均を求めたものです。MSE は以下の式で表されます。

    $$\mathrm{MSE}=\frac{1}{n}\sum _{i=1}^n{(y_i-{\hat{y}}_i)}^2$$
  

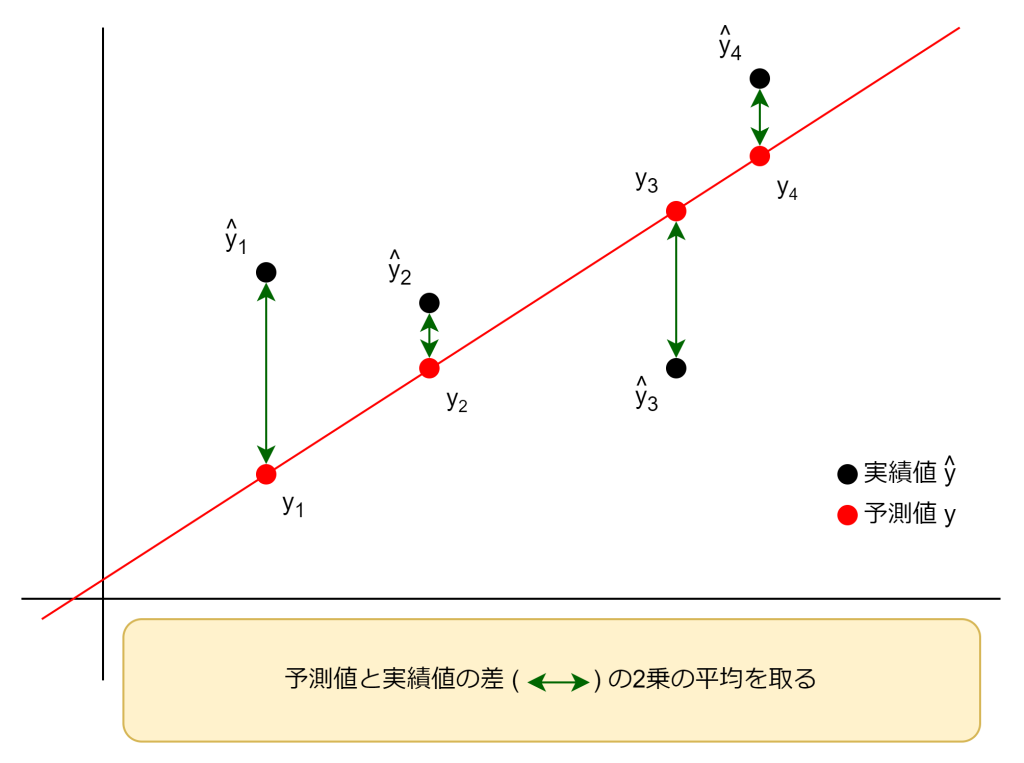
MSEは誤差が大きいほど値が大きくなり、外れ値の影響を受けやすい特徴があります。誤差が大きいサンプルが重要な場合や、外れ値を重視してモデルを評価・改善したい場合に適しています。ただし、値の単位が元データの単位の二乗になるため、直感的な解釈はやや難しくなります。モデルの予測精度を比較する際に、MSE が小さいほど良いモデルと判断されます。

二乗平均平方根誤差 (RMSE)

二乗平均平方根誤差（RMSE）は、平均二乗誤差（MSE）の平方根を取った評価指標です。RMSE は誤差の大きさを元のデータと同じ単位で表すため、直感的に解釈しやすい特徴があります。値が小さいほどモデルの予測精度が高いと判断できます。

    $$\mathrm{RMSE}=\sqrt{\mathrm{MSE}}=\sqrt{\frac{1}{n}\sum _{i=1}^n{(y_i-{\hat{y}}_i)}^2}$$
  

MSEの平方根を取ることで、元データと同じ単位で誤差を評価できます。外れ値の影響を受けやすい点はMSEと同様ですが、誤差の大きさを直感的に把握したい場合や、実際のデータのスケールで評価したい場合に適しています。多くの実務で標準的に用いられる指標です。

平均絶対値誤差 (MAE)

平均絶対値誤差（MAE）は、予測値と実測値の差（残差）の絶対値を平均した指標です。MAE は以下の式で表されます。

    $$\mathrm{MAE}=\frac{1}{n}\sum _{i=1}^n|y_i-{\hat{y}}_i|$$
  

誤差の絶対値の平均を取るため、MAEは外れ値の影響を受けにくく、誤差の平均的な大きさを直感的に把握できる特徴があります。誤差の分布に外れ値が多い場合や、平均的な誤差の大きさを重視したい場合に適しています。値の解釈も直感的です。

おわりに

外れ値を重視するなら平均二乗誤差(MSE)や二乗平均平方根誤差(RMSE)、外れ値の影響を抑えたい場合は 平均絶対値誤差(MAE)を選ぶとよいでしょう。モデルの用途やデータの特性に応じて、適切な指標を選択することが重要です。

ではまた。