階層ありクラスタリングでクラスタを階層構造に分類する

皆さん、こんにちは。LP開発グループのn-ozawanです。
私たちにとって猫は身近な動物ですが、日本の侵略的外来種ワースト100にも選ばれており、元々、日本に生息していない動物です。

本題です。
教師なし学習の分野にはクラスタリング手法が存在しますが、大きく分けて階層構造を持たないクラスタリングと、階層構造を持つクラスタリングの2種類があります。前回お話ししたk-means法は階層構造を持たないクラスタリングです。今回は階層構造を用いてクラスタリングを行う「階層ありクラスタリング」についてのお話です。

階層ありクラスタリング

概要

階層ありクラスタリングは、データを階層構造でグループ化する手法です。教師なし学習の一種で、データの関係性や類似性を分析する際に利用されます。

例えば、顧客データを分析し、類似した購買行動や属性を持つグループを特定することで、より細かなサービスを提供できるようになります。他にも、類似した文書を効率的に整理したり、異常検知に利用されることもあります。

以前取り上げたk-means法は階層なしクラスタリングと呼ばれ、単にクラスタを分類するだけです。一方で、階層ありクラスタリングは、クラスタを階層構造により分類します。この階層構造は樹形図で表現することができ、これをデンドログラムと言います。

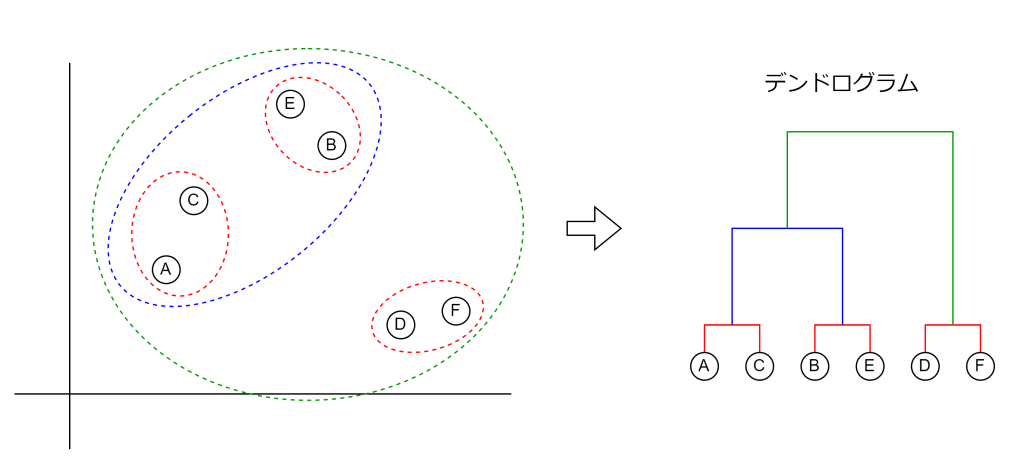
階層ありクラスタリングは距離の近いデータおよびクラスタ同士を、新しいクラスタとして結合します。この「距離の近い」をどのように解釈するのかで様々な手法が存在します。今回は最短距離法とウォード法について取り上げたいと思います。

最短距離法

最短距離法は、いたってシンプルで、2つのデータもしくはクラスタ間の最も近い距離を基準にクラスタを統合する手法です。この手法は、細長い形状のクラスタを生成しやすく、データが連続的に分布している場合に適しています。ただし、ノイズや外れ値の影響を受けやすいという欠点があります。

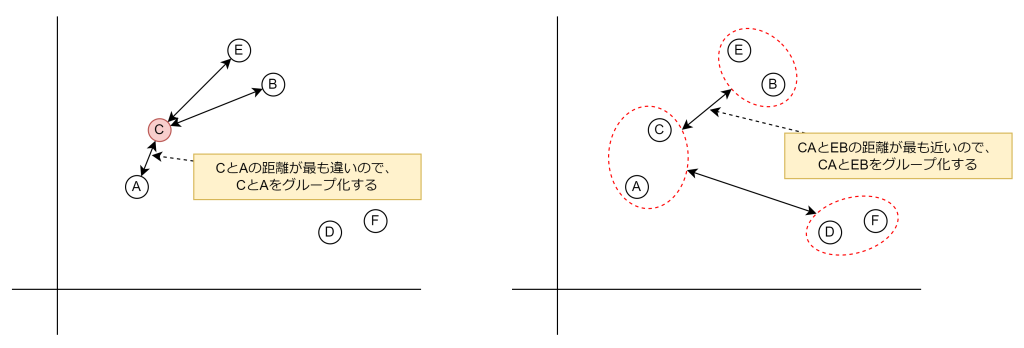
ウォード法

ウォード法は、クラスタ内の分散の増加を最小となるような、近いクラスタ同士を統合する手法です。この手法では、統合後のクラスタ内の分散が最も小さくなるように選択するため、クラスタリング結果は比較的均一なサイズのクラスタを生成しやすく、データの分布が均等である場合に適しています。

ウォード法における2つのクラスタ（C1とC2）の距離は、以下の計算式で求められます。

$d(C_1,C_2)=L(C_1\cup C_2)-L\left(C_1\right)-L\left(C_2\right)$

L(C)は、クラスタC内のばらつきを表す指標であり、具体的には重心からの距離の二乗和を指します。式中の「∪」は和集合を意味し、C₁ ∪ C₂ はクラスタC₁とC₂を統合したクラスタを表します。この距離が最も近いクラスタ同士を統合します。

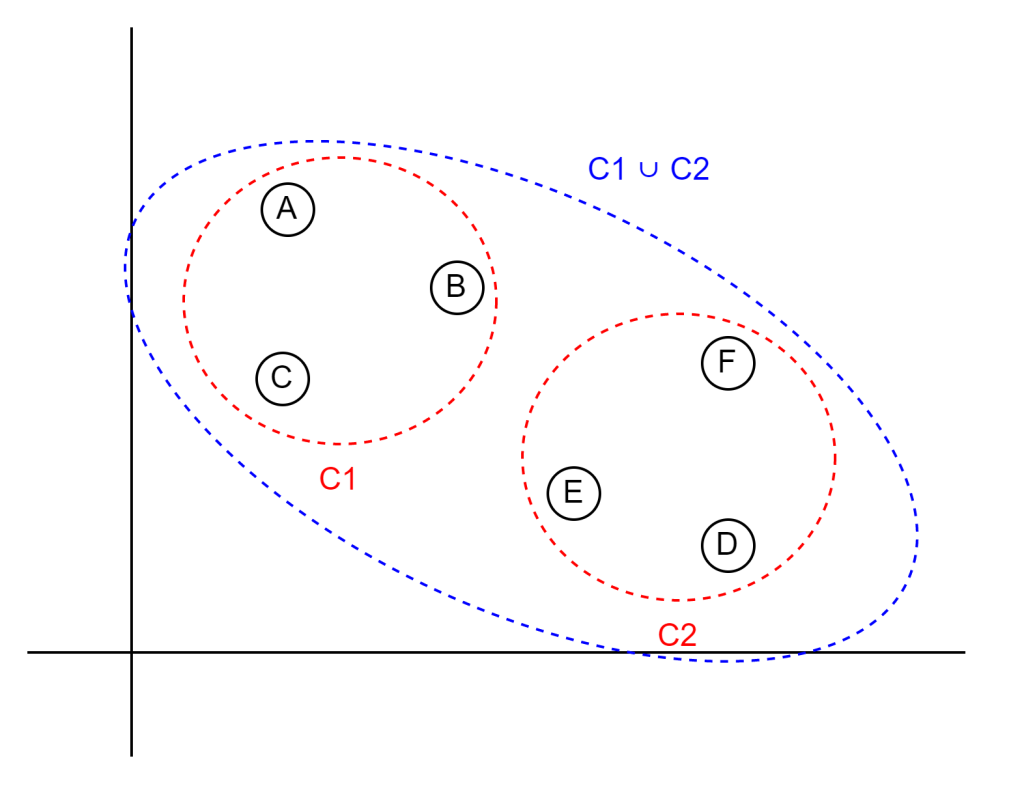
先ほどの計算式をグラフで表現すると以下のようになります。

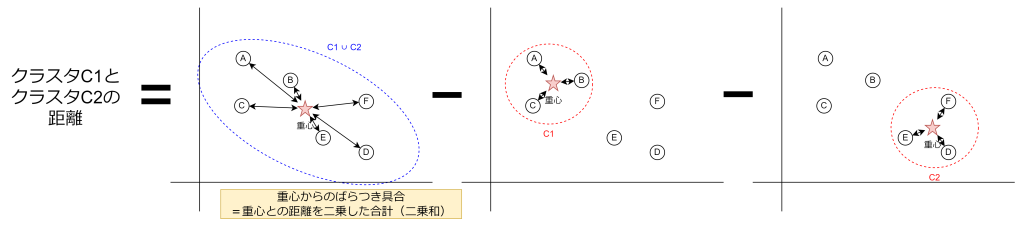
おわりに

ウォード法はクラスタ内の分散を重視するため、均一なサイズのクラスタを生成する傾向があります。一方、最短距離法は局所的な距離に基づいてクラスタを統合するため、細長い形状のクラスタを生成しやすい特徴があります。どの手法を選択するかは、データの特性や分析の目的に応じて決定する必要があります。

ではまた。