単回帰の線形回帰を実装してみる

皆さん、こんにちは。技術開発グループのn-ozawanです。
キャベツが安くなりましたね！キャベツはそのまま千切りにしてもいいし、炒め物や煮物でも活躍します。この時期であれば春キャベツと新玉ねぎを使ったポトフも美味しいです。

本題です。
前回、線形回帰に関する基本的な知識を整理しました。今回は線形回帰を求める手法を紹介しつつ、実際にコーディングしてみたいと思います。

単回帰分析

最小二乗法

単回帰分析は、1つの説明変数と1つの目的変数の関係を分析する手法であり、X軸とY軸の二次元で表現することができます。よって、単回帰の線形回帰はy = ax + bの一次関数で表すことができます。この式におけるaは傾きであり、bは切片と言います。このaとbを求めることで、x（説明変数）が与えられたときの、y（目的変数）を導くことができるようになります。

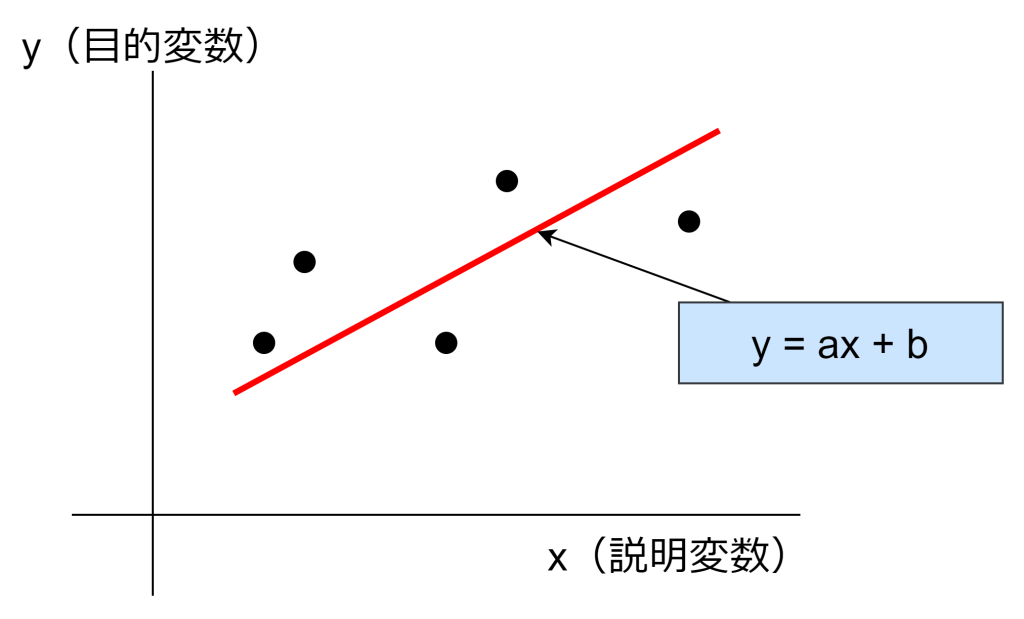
このa（傾き）とb（切片）のことを回帰係数と呼ばれ、多くの場合、最小二乗法により求めます。最小二乗法とは、y（目的変数）と直線の差を二乗して合計した値が最小となるように、最もらしい線を引く手法です。

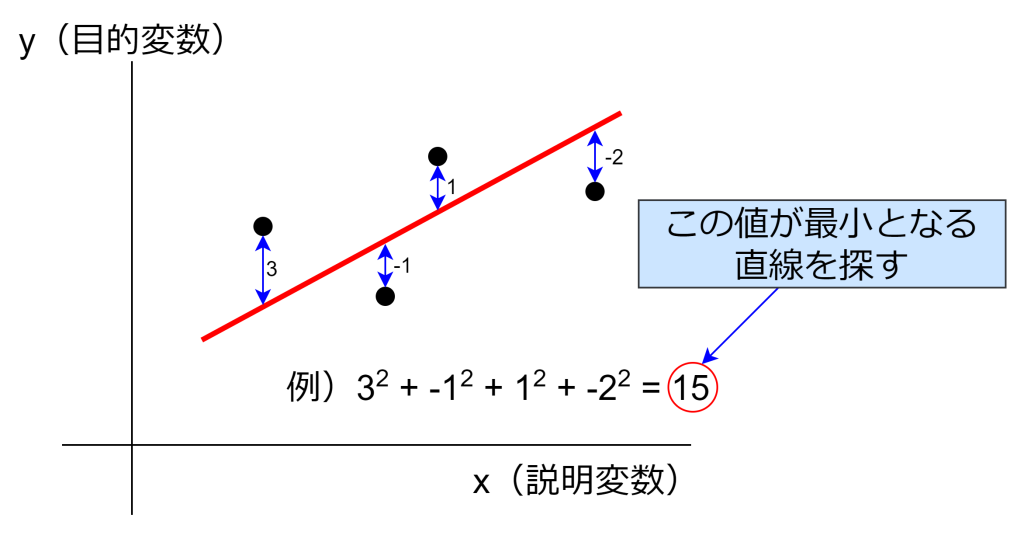
「y（目的変数）と直線の差を二乗して合計した値が最小」となる値を求めるには、偏微分を用いて傾きが0になる値を探します。この偏微分を解くことで以下の式となり、aとbの値を求めることができるようになります。

$''a（傾き）''=\frac{''xとyの共分散''}{''xの分散''}$
$''b（切片）''=''yの平均''-(''a（傾き）''\times ''xの平均'')$

分散とは？

分散はデータのばらつきを表す指標の一つであり、データが平均値からどれだけ離れているかを示します。具体的には、各データ点と平均値との差を二乗した値の平均を計算することで求められます。分散が大きいほどデータのばらつきが大きく、小さいほどデータが平均値の近くに集中していることを意味します。

例えば、とある5人のクラスでテストが行われ、それぞれ90点、70点、40点、30点、60点というケースを考えます。各点数と平均点との差を二乗した値の平均は456となり、分散は456となります。

$''平均''=\frac{''合計''}{\mathrm{人数}}=\frac{(90+70+40+30+60)}{5}=58$
$''分散''=\frac{''各点数と平均点との差を二乗した値の合計''}{\mathrm{人数}}$
$=\frac{{(\mathrm{90}-\mathrm{58})}^2+{(\mathrm{70}-\mathrm{58})}^2+{(\mathrm{40}-\mathrm{58})}^2+{(\mathrm{30}-\mathrm{58})}^2+{(\mathrm{60}-\mathrm{58})}^2}{5}=456$

なお、この分散の平方根を標準偏差と言います。分散と一緒に覚えておくとよいでしょう。

$''標準偏差''=\sqrt{''分散''}$

共分散とは？

共分散は、2つの変数xとyがどのように連動して変化するかを示す指標です。具体的には、xの偏差とyの偏差を掛け合わせた値の平均を計算することで求められます。偏差とは、その値と平均との差です。共分散が正の値であれば、2つの変数は同じ方向に変化する傾向があり、負の値であれば逆方向に変化する傾向があることを意味します。

例えば、とある5人のクラスでテストが行われ、それぞれ国語が90点、70点、40点、30点、60点、数学が70点、80点、60点、20点、40点というケースを考えます。この場合、共分散は328となり、国語の点数と数学の点数で関連性があるとみることができます。

$''国語の平均点''=\frac{''合計''}{\mathrm{人数}}=\frac{(90+70+40+30+60)}{5}=58$
$''数学の平均点''=\frac{''合計''}{\mathrm{人数}}=\frac{(70+80+60+20+40)}{5}=54$
$''Aさんの各変数の偏差の積''=(\mathrm{90}-\mathrm{58})\times (\mathrm{70}-\mathrm{54})=\mathrm{512}$
$''Bさんの各変数の偏差の積''=(\mathrm{70}-\mathrm{58})\times (\mathrm{80}-\mathrm{54})=\mathrm{312}$
$''Cさんの各変数の偏差の積''=(\mathrm{40}-\mathrm{58})\times (\mathrm{60}-\mathrm{54})=\mathrm{-108}$
$''Dさんの各変数の偏差の積''=(\mathrm{30}-\mathrm{58})\times (\mathrm{20}-\mathrm{54})=\mathrm{952}$
$''Eさんの各変数の偏差の積''=(\mathrm{60}-\mathrm{58})\times (\mathrm{40}-\mathrm{54})=\mathrm{-28}$
$''共分散''=\frac{''各変数の偏差の積の合計''}{\mathrm{人数}}=\frac{\mathrm{512}+\mathrm{312}+\mathrm{-108}+\mathrm{952}+\mathrm{-28}}{5}=328$

計算してみる

話を戻して、実際に計算してみましょう。以下のデータの回帰係数を求めます。

まずは「xの分散」を求めます。x（説明変数）は身長です。

$''身長の平均''=\frac{''合計''}{\mathrm{人数}}=\frac{(160+170+180+150+165)}{5}=165$
$''身長の分散''=\frac{''各身長と平均身長との差を二乗した値の合計''}{\mathrm{人数}}$
$=\frac{{(160-165)}^2+{(170-165)}^2+{(180-165)}^2+{(150-165)}^2+{(165-165)}^2}{5}$
$=\frac{25+25+225+225+0}{5}=100$

次に「xとyの共分散」を求めます。y（目的変数）は体重です。

$''体重の平均''=\frac{''合計''}{\mathrm{人数}}=\frac{(50+68+76+45+53)}{5}=58.4$
$''共分散''=\frac{''各身長と平均身長の偏差と各体重と平均体重の偏差の積の合計''}{\mathrm{人数}}$
$=\frac{(160-165)\times (50-58.4)+(170-165)\times (68-58.4)+(180-165)\times (76-58.4)+(150-165)\times (45-58.4)+(165-165)\times (53-58.4)}{5}$
$=\frac{(-5\times -8.4)+(5\times 9.6)+(15\times 17.6)+(-15\times -13.4)+(0\times -5.4)}{5}$
$=\frac{42+48+264+201+0}{5}=111$

a（傾き）とb（切片）を求めます。

$''a（傾き）''=\frac{''xとyの共分散''}{''xの分散''}=\frac{111}{100}=1.11$
$''b（切片）''=''yの平均''-(''a（傾き）''\times ''xの平均'')=58.4-(1.11\times 165)=-124.75$

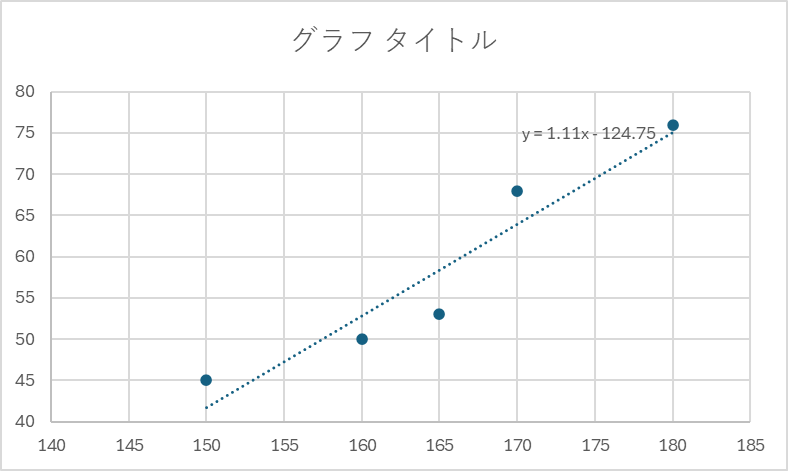
aが1.11、bが-124.75と求められました。Excelで同じデータを使用してグラフを作成し、近似曲線（線形）を表示すると、今回求めたaとbと一致する直線が引かれていることが確認できます。

Pythonで実装してみる

pythonのコードは以下の通りです。分散や共分散などの計算にはnumpyを利用しています。

import numpy as np

# データ
heights = np.array([160, 170, 180, 150, 165])  # 身長
weights = np.array([50, 68, 76, 45, 53])       # 体重

# 平均を計算
mean_height = np.mean(heights)
mean_weight = np.mean(weights)

# 身長の分散を計算
height_variance = np.var(heights)

# 共分散を計算
covariance = np.cov(heights, weights, bias=True)[0][1]

# 傾き a を計算
a = covariance / height_variance

# 切片 b を計算
b = mean_weight - a * mean_height

# 結果を表示
print(f"傾き a: {a}")
print(f"切片 b: {b}")

おわりに

今回は線形回帰のロジックを理解するために、numpyを使ってコーディングしました。実際はScikit-learnなどの機械学習ライブラリがありますので、そちらを使用する方が良いか思います。

ではまた。