線形回帰の基本をまとめてみた

皆さん、こんにちは。技術開発グループのn-ozawanです。
本ブログも投稿を始めてから2周年となりました。まだまだカーニアン多雨事象の100万分の1程度ではありますが、今後ともよろしくお願いいたします。

本題です。
当社では生成AIの利用を推進し、業務効率の向上や新たなサービス創造を目指しています。それに先立ち、今年からAIを勉強しているのですが、なかなか難しいですね。今回は機械学習の基本ともいえる線形回帰について、まずは基本的なところから学びたいと思います。

回帰分析

概要

回帰分析は、データ間の関係性を分析し、予測や推定を行うための統計手法です。主に、説明変数と目的変数の間の関係を明らかにすることを目的とします。

説明変数は、モデルにおいて予測や説明の基礎となる変数です。目的変数は、説明変数の影響を受けた結果として観測される変数です。例えば、気温（説明変数）がアイスクリームの売上（目的変数）に与える影響を調べる場合、気温が変化することで売上がどのように変動するかを分析します。このように、説明変数と目的変数の関係を明らかにすることで、データの背後にある因果関係やパターンを理解することが可能になります。

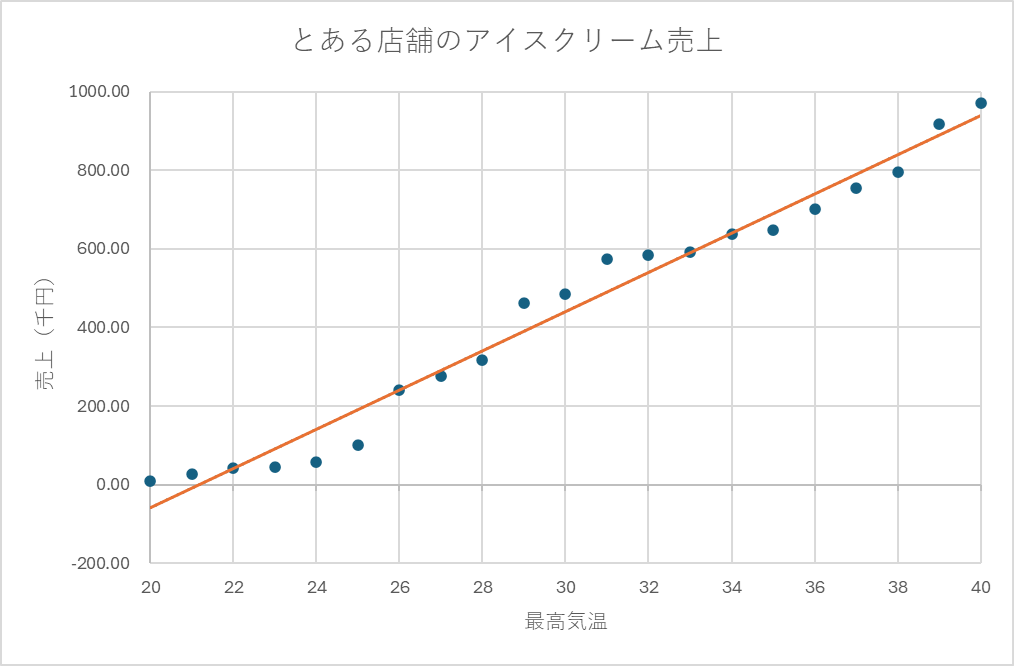
回帰分析により、過去のデータを基に将来の値を予測したり、変数間の影響を評価したりすることが可能になります。

線形回帰と非線形回帰

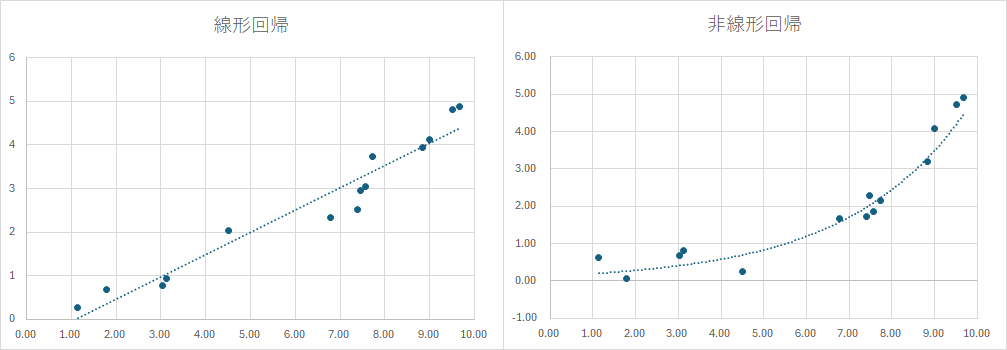
線形回帰は、説明変数と目的変数の間の関係が直線で表される場合に使用されます。単回帰分析（後述）であれば、直線はy = ax + b のような式で表現されます。線形回帰は計算が比較的簡単で、結果の解釈もしやすいため、広く利用されています。

一方、非線形回帰は、説明変数と目的変数の関係が直線では表せない場合に使用されます。このモデルでは、関係性が曲線や複雑な関数で表現されます。例えば、指数関数や対数関数などの式で表現されます。

単回帰分析と重回帰分析

単回帰分析は、1つの説明変数と1つの目的変数の関係を分析する手法です。これまで述べてきた例はすべて単回帰分析に該当し、XとYのグラフで視覚的に表現することができます。この手法はシンプルで計算が容易なため、基本的な分析に適しています。

一方、重回帰分析は、複数の説明変数と1つの目的変数の関係を分析する手法です。例えば、広告費、気温、季節（説明変数）が売上（目的変数）に与える影響を同時に調べる場合、重回帰分析を用います。この手法により、複数の要因が目的変数にどのように影響を与えるかを評価することが可能です。重回帰分析は、より複雑なデータや多次元的な関係を扱う際に有用です。

おわりに

単回帰分析は2次元なので、XとYのグラフでイメージしやすいですが、重回帰分析は多次元なので、なかなかイメージが湧きません。まずはシンプルな単回帰分析で理解を深めていきたいと思います。と言うことで、次回は単回帰分析をPythonで実装したいと思います。

ではまた。