探索木について改めて理解する

皆さん、こんにちは。技術開発グループのn-ozawanです。
もし地球を原子サイズ（約0.0000000001m）に縮小した場合、現在の観測可能な宇宙は約700万kmとなり、地球と月の距離の約18倍に相当するのだそうです。

本題です。
1950年代後半あたりに起きた第1次AIブームは「推論・探索の時代」とも呼ばれています。まさに探索木はその時代で研究が進み、第1次AIブームを牽引しました。探索木はブームが去った今でも研究が続けられており、数多くのシステムで使われています。今日はそんな探索木についてまとめてみました。

探索木

概要

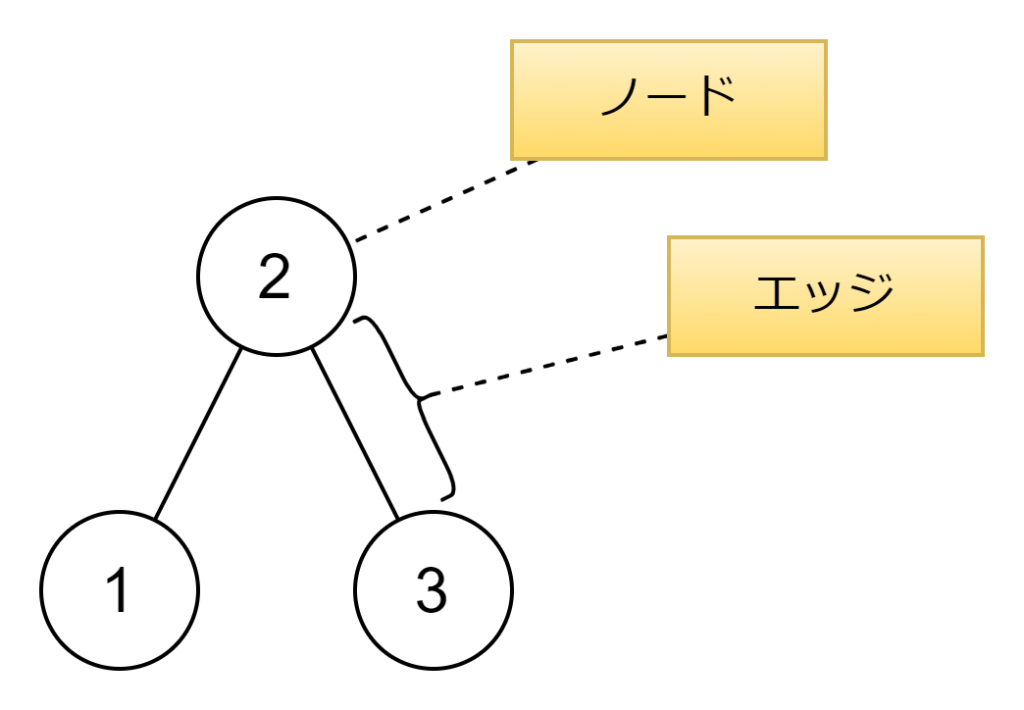
探索木は、特定の条件に基づいてデータを効率的に探索するための木構造です。木構造は、ノードと呼ばれる要素と、それらを接続するエッジから構成されます。各ノードにはデータが格納されており、エッジはノード間の関係を示します。

1950年代後半に起きた第1次AIブームで、探索アルゴリズムなどが注目され、探索木を用いた問題解決が盛んに研究されました。第1次AIブームは迷路などの簡単な問題（トイ・プロブレム）しか解決できなかったために下火になりましたが、探索木はデータベース、ファイルシステム、ネットワークルーティングなど、さまざまな分野で今でも広く利用されています。

種類

探索木の代表的な種類に以下があります。

二分探索木

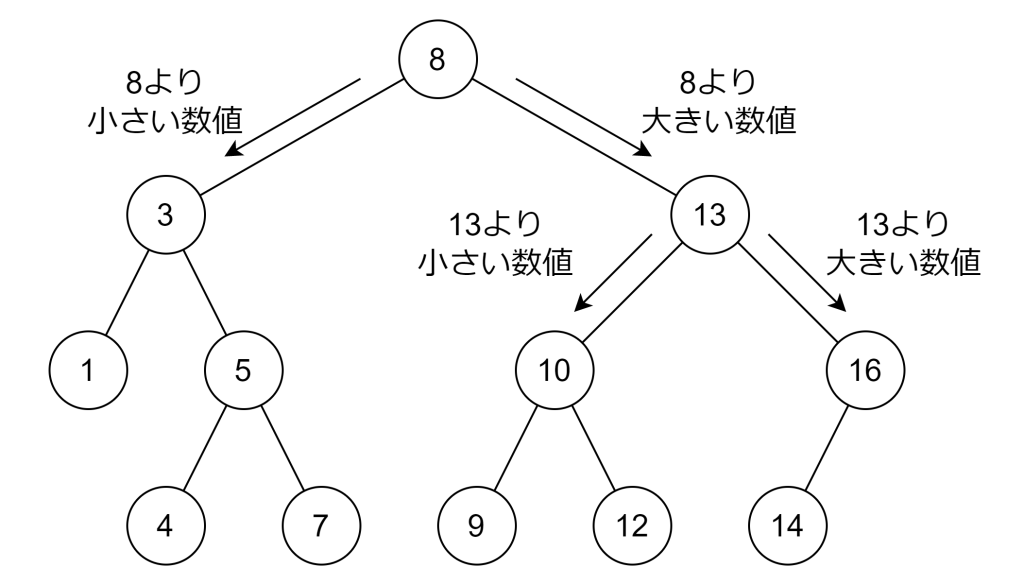
二分探索木は、各ノードが最大で2つの子ノードを持つ木構造です。二分探索木の特徴は、左の子ノードの値が親ノードの値よりも小さく、右の子ノードの値が親ノードの値よりも大きいという点です。この特性により、データの検索、挿入、削除が効率的に行えます。

B木

B木は多分岐の探索木です。B木の各ノードには複数のキーが格納されており、キーの値に基づいて子ノードへのポインタが配置されます。データベースやファイルシステムで利用されています。

トライ木

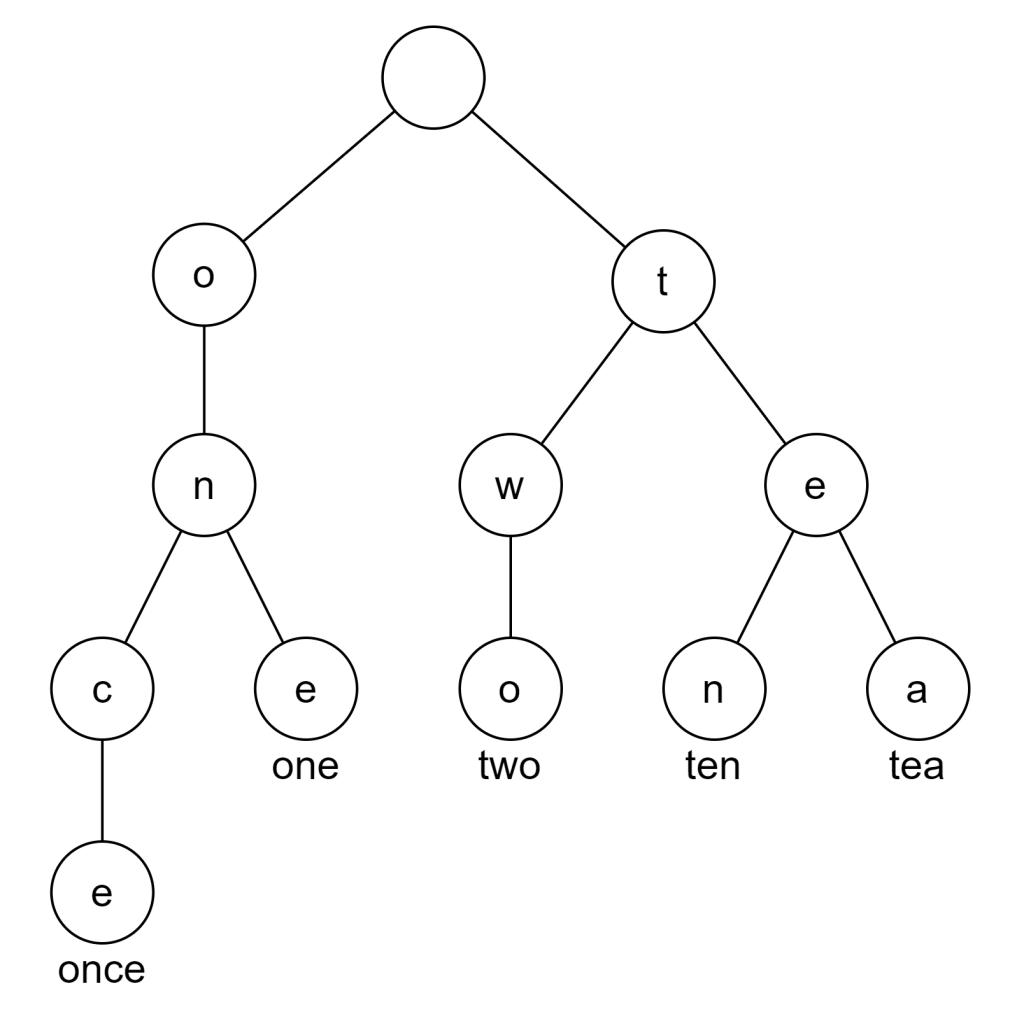
トライ木は文字列を効率的に検索するための木構造です。文字列検索や補完、辞書などに利用されています。以下の例はone（一）、once（1回）、two（二）、ten（十）、tea（紅茶）をトライ木で表現したものです。

探索木で迷路を解く

先ほども述べた通り、探索木は第1次AIブームにて盛んに研究されました。探索木は迷路を解く際にも活用されます。例えば、以下の迷路があるとします。迷路はSから始まり、Gでゴールします。

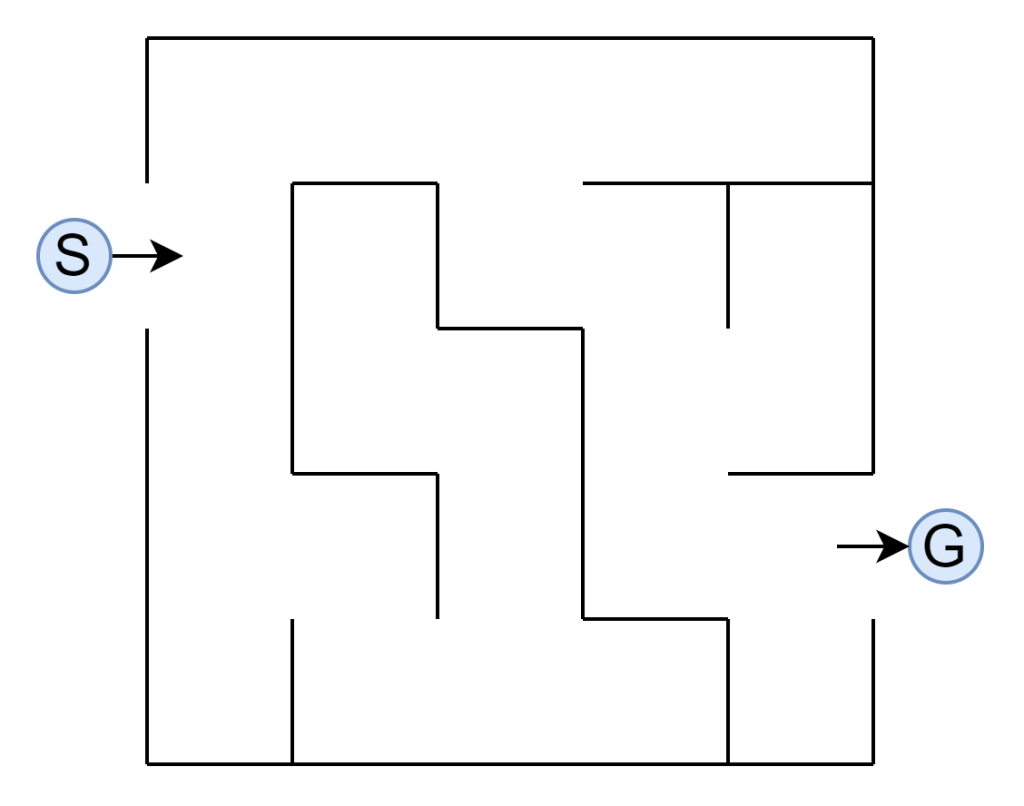
上記の迷路に対して分岐と行き止まりに記号を付けて線で繋げます。

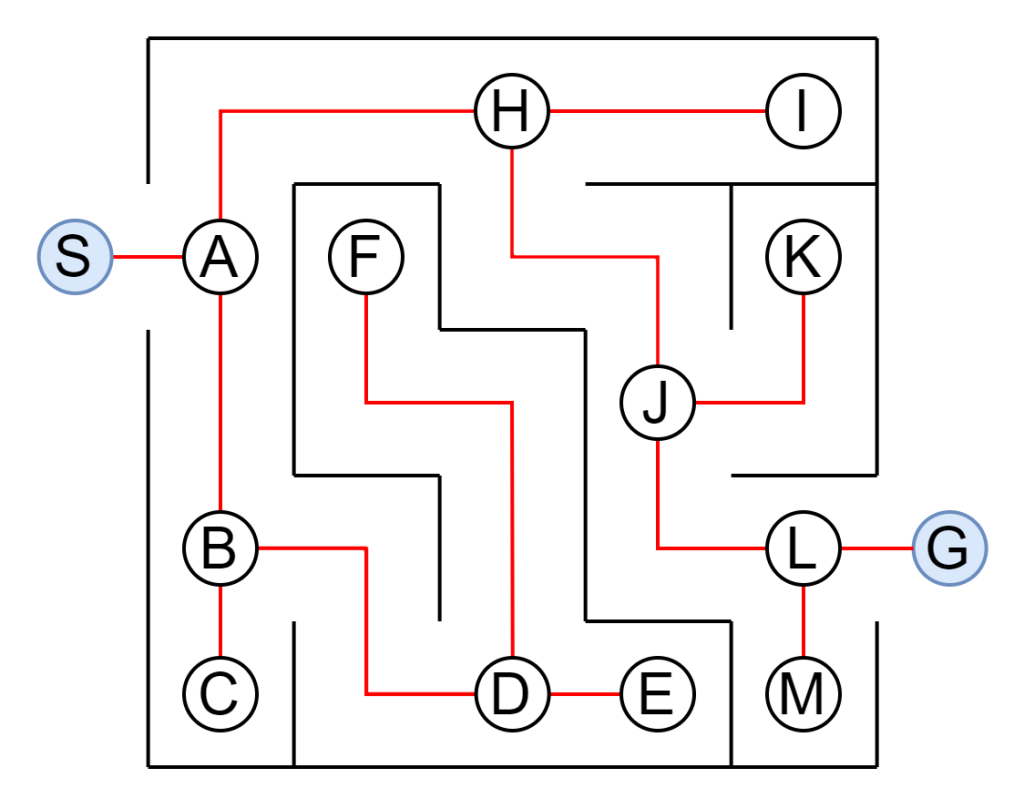
各記号とのつながりを整理すると木構造となります。SからGへの道順を辿ればゴール出来るというわけです。

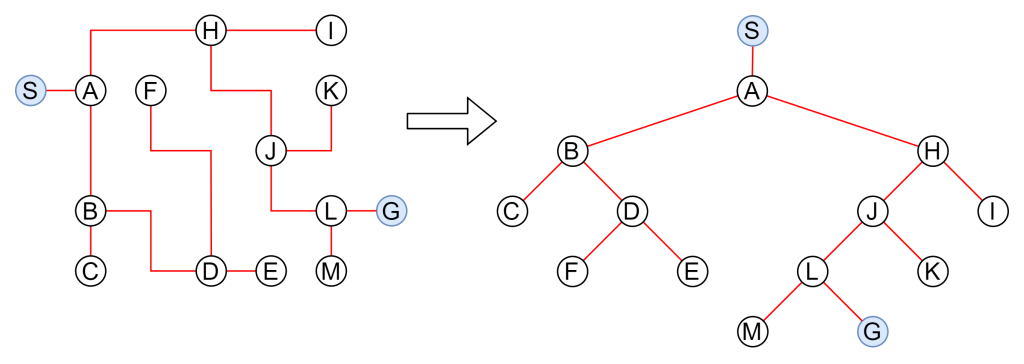
「道順を辿れば」と言いましたが、人の目で見れば一目瞭然ですが、コンピュータはそうはいきません。上記の木構造は、二分探索木のように探索しやすいように工夫されていませんので、簡単に道順を辿ることは出来ません。

深さ優先探索

深さ優先探索は最下層まで探索を進め、行き止まりに達したら1個戻って別の経路を探索します。行き止まりに遭遇するまで突き進むイメージです。メモリ使用量が少なく済むというメリットがある一方で、探索木が非常に深い場合は探索に時間がかかるというデメリットもあります。

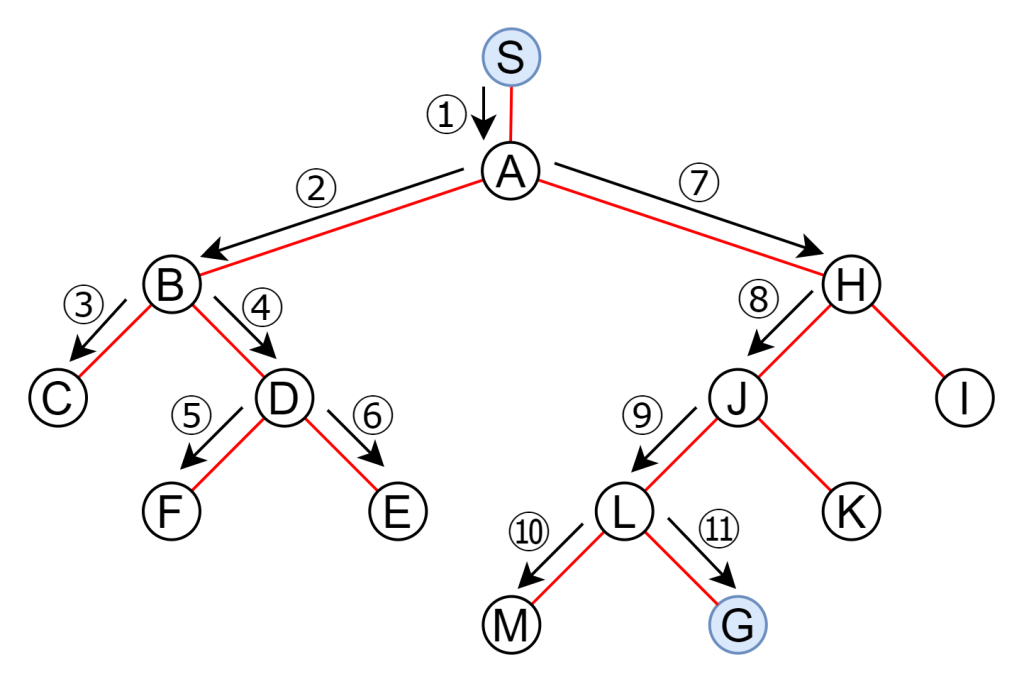
幅優先探索

幅優先探索は隣接するノードをすべて探索してから、その次のノードを探索します。分岐路までを正確にマッピングしながら慎重に進むイメージです。迷路でゴールまでの道順に複数の経路がある場合、最短経路を見つけ出すことが出来る一方で、多くのメモリを必要とします。

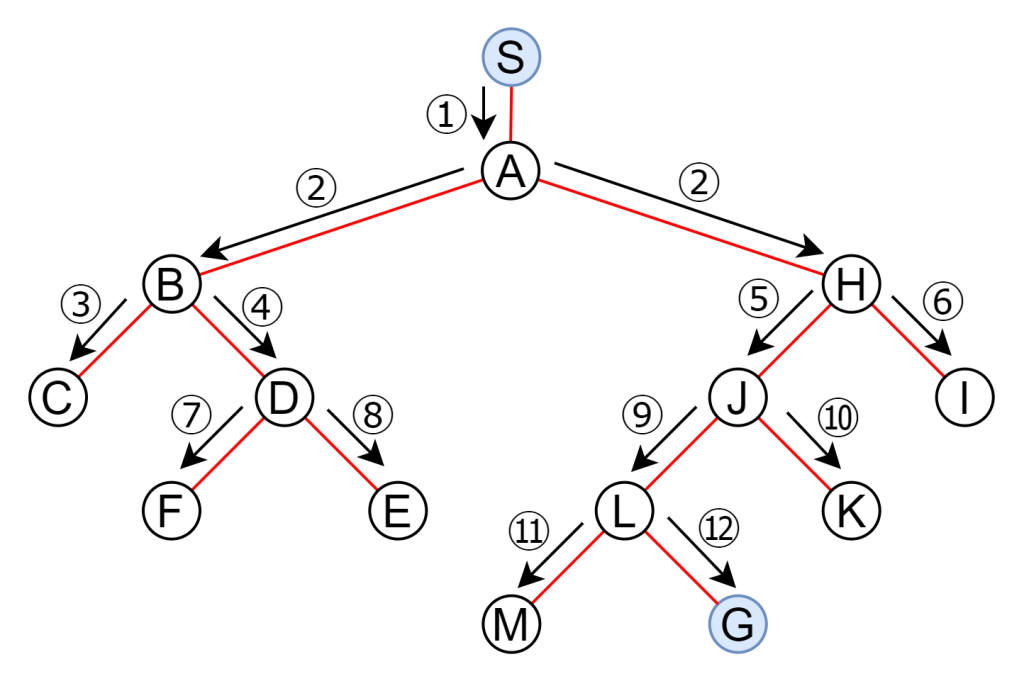
おわりに

昨今のプログラムはライブラリが充実しているため、探索木を1からコーディングする機会はないかと思います。しかし、探索木は性能に直結しますので、しっかりと理解することが重要です。

ではまた。