C言語で64bitを超える数値を計算する方法
皆さん、こんにちは。技術開発グループのn-ozawanです。
GW楽しんでますか?「ゴールデンウィーク」という言葉は1952年ごろから登場したと言われているので、もう70年以上の歴史があるんですね。
本題です。
たまには実用性のないネタをしれっと投稿したい今日この頃。みなさん、C言語が扱える最大値はいくつかご存知でしょうか。そうです。unsigned long long型の64bitで、最大で18,446,744,073,709,551,615まで扱えます。1844京6744兆737億955万1615です。でも64bitを超える数値を扱いたいときってありませんか?今日はそのやり方をお話しします。
目次
桁数が多い数値
冒頭でもお話しした通り、unsigned long long型の64bitで、最大で1844京6744兆737億955万1615まで表現できます。十分大きな数値なので、これ以上の数値を扱うケースは中々ないのですが、もし、64bitを超える数値を扱う場合、どうすればよいでしょうか?
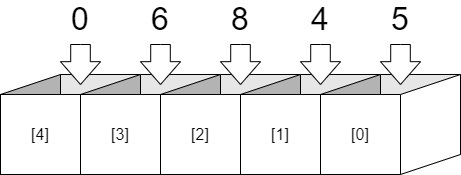
C言語で64bitを超える数値を扱う場合は配列を用います。例えば”6845″という数値を扱う場合、数値を以下のように格納します。注意点は1桁目を配列要素の0番に格納していることです。これであればメモリが許す限り何桁でも表現が出来ます。
#include <stdio.h>
#define NUMBER_OF_DIGITS 30
void main() {
unsigned char value[NUMBER_OF_DIGITS] = {5, 4, 8, 6}; // 6845
// 数値をコンソールに表示
for (int i = NUMBER_OF_DIGITS - 1; i >= 0; i--) {
printf("%d", value[i]);
}
printf("\n");
}加算
さて、数値の表現はこれで解決しました。次は足し算をしましょう。これはそんなに難しい話ではありません。繰り上がりを考慮しながら一桁ずつ足していけばOKです。
void sum(unsigned char* v1, unsigned char* v2, unsigned char* result) {
bool carry = false; // 繰り上げフラグ (true = 繰り上げあり、false = 繰り上げなし)
for (int i = 0; i < NUMBER_OF_DIGITS; i++) {
int sum = v1[i] + v2[i] + (carry ? 1 : 0);
carry = (sum >= 10);
result[i] = sum % 10;
}
}減算への考察
さて次は引き算をしてみましょう。足し算の時はcarryフラグで繰り上げを制御することで計算していました。引き算も同様にフラグ制御で繰り下げをすれば良さそうに見えますが、そう簡単には行きません。足し算の繰り上げは単純に次の桁の計算で+1をするだけに対して、引き算の繰り下げは次の桁が0の場合に限り、それ以降も-1する必要があります。
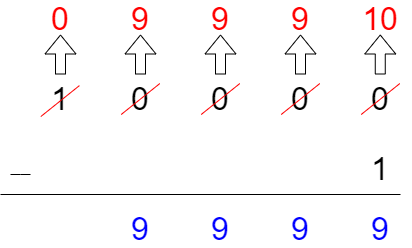
実際にコーディングしてみると分かるのですが、制御が複雑になります。また、この問題を解決しても、「101 – 10000」のようなv1 < v2の計算を考慮しなくてはなりません。中々骨が折れそうです。
補数
減算の処理が難しそうだ、ということが分かりました。では、どうすればいいのでしょうか。実はCPUは減算する回路がありません。減算も含めて、すべて加算とbit反転で解決しています。例えば「72 – 25」という式は、「72 + (-25)」と同じです。「72」に対して「-25」を加算すればよいのです。では、「-25」をCPUはどうやって表現しているのでしょうか?
CPUは「-25」のような負の値を補数で表現しています。補数とは、その数値に対して、足し合わせるとちょうど桁が一つ増える最小の数のことを言います。例えば「7」の場合、「3」を足せば「10」になります。この場合、「7」の補数は「3」になります。
CPUは数値を2進数で計算します。例えば「25」を2進数で表現すると「0001 1001」です。「0001 1001」に対して「1110 0111」を足すとちょうど「1 0000 0000」となり、桁が1つ増えます。この場合、「0001 1001」の補数は「1110 0111」になります。CPUはこの補数である「1110 0111」を「-25」として扱います。
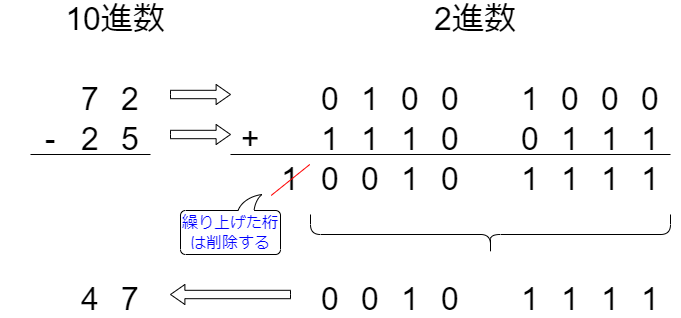
先ほどの「72 + (-25)」を実際に計算してみましょう。「72」の2進数は「0100 1000」です。「-25」の2進数の補数は「1110 0111」ですね。これを足すと「1 0010 1111」となります。繰り上がった分を削除した「0010 1111」が減算の答えになります。「0010 1111」を10進数にすると「47」ですね。CPUは、補数を足すことにより減算処理を行っているのです。
2の補数と10の補数
2進数の補数を「2の補数」、10進数の補数を「10の補数」と呼びます。補数を足せば引き算が出来るのは先に述べた通りです。10の補数を求められれば引き算が出来るようになります。この補数、どうやって求めればいいのでしょうか?
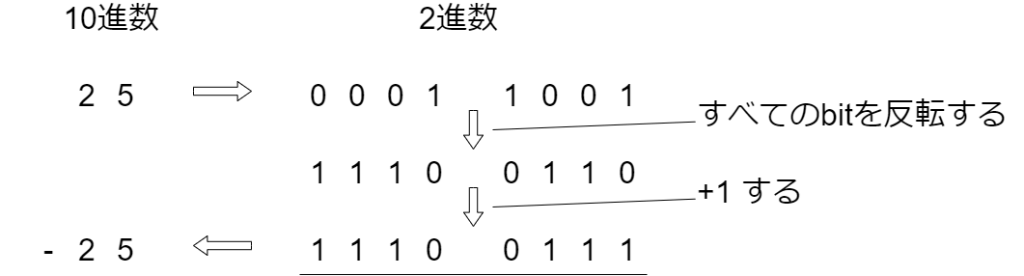
2の補数は以下の手順となります。
1. すべてのbitを反転する
2. 手順1の結果に対して+1する
10の補数は、その数値から1つ桁が多い最小の数値から引きます。例えば「25」の数値であれば、100 – 25で、「75」という補数が得られます。しかし先ほど述べた通り、繰り下げが発生する引き算は出来ません。なので、以下の手順を取ります。
1. その数値と同じ桁数で最大の数値から引く
2. 手順1の結果に対して+1する

「その数値と同じ桁数で最大の数値から引く」がミソです。これであれば繰り下げは発生しません。単純にすべての桁に対して9から引けばいいだけです。ではこの10の補数で実際に計算してみましょう。「72 + (-25)」は「72 + 75」となり結果は「147」となります。溢れた桁を捨てれば「47」になります。計算できてそうですね!
減算
引き算をするための情報が出揃いました。早速引き算をコーディングしてみましょう。
void changeSign(const unsigned char* v1, unsigned char* result) {
unsigned char one[NUMBER_OF_DIGITS] = {1};
unsigned char temp[NUMBER_OF_DIGITS] = {};
for (int i = 0; i < NUMBER_OF_DIGITS; i++) {
temp[i] = 9 - v1[i];
}
sum(temp, one, result);
}
void sub(const unsigned char* v1, const unsigned char* v2, unsigned char* result) {
unsigned char temp[NUMBER_OF_DIGITS] = {};
sign(v2, temp);
sum(v1, temp, result);
}changeSign関数は補数を求める関数でもあるのですが、それと同時に補数から元の数値に戻すことも出来ます。つまり、正の値と負の値を変換する処理(+ ↔ -)となっています。sub関数は減算ですね。符号を変換(正の値であれば負の値に、負の値であれば正の値に変換)して足しているだけです。
負の値をコンソールに表示するようにしましょう。先ほどの例だと「25」の補数は「75」です。しかしコンソールには「75」ではなく「-25」と表示したいですよね。
bool isMinus(const unsigned char* v1) {
return v1[NUMBER_OF_DIGITS - 1] == 9;
}
void print(const unsigned char* v1) {
unsigned char temp[NUMBER_OF_DIGITS] = {};
if (isMinus(v1)) {
printf("-");
sign(v1, temp);
} else {
printf("+");
memcpy(temp, v1, NUMBER_OF_DIGITS);
}
for (int i = NUMBER_OF_DIGITS - 1; i >= 0; i--) {
printf("%d ", temp[i]);
}
printf("\n");
}isMinus関数はその値が負の値かどうかを判定します。配列要素を符号判定用に1つ余分に持たせることにより、0か9かで正か負かを判定することが出来ます。例えば「025」の補数は「975」となります。あとはその情報を元にコンソールに表示して上がれば完了です。
おわりに
いかがでしたでしょうか。CPUの性能を超えて、100桁以上の数値でも計算が出来るようになります。ただ、JavaやC#であれば、BigIntegerという何桁でもOKなクラスが既にありますし、そもそも京を超える数値を計算したいケースがあまりないことから、残念ながら実用性はほぼ0です。
今回は加算(足し算)と減算(引き算)を紹介しましたが、他にも積算(掛け算)と除算(割り算)がありますので、時間がある方はぜひチャレンジしてみてください。
今回紹介したプログラムはまだ課題が残っています。char型は1byte(0 ~ 255)までを表現する変数に対して、0 ~ 9の10パターンしか格納していません。つまり、246パターン分が使われておらず、メモリを無駄に消費しています。この課題の解消は簡単です。今回は10進数で計算してましたが、256進数で計算すればよいのです。暇な人、レッツトライ!

 アイオス コーポレートブログ
アイオス コーポレートブログ
















